Самый веселый и замечательный праздник, который многие ждут с нетерпением, Новый год. С раннего детства любимое занятие большинства – украшение праздничной ёлки. Новогодние стеклянные игрушки имеют свойство разбиваться, поэтому каждый год стоит проблема — покупка новых. А можно найти другой выход из положения: сделать игрушки. Кроме традиционных елочных украшений (хлопушек и фонариков) можно сделать «геометрические» игрушки. Особенно красивы модели правильных многогранников (Платоновы тел) сделанных из цветной бумаги.

На рисунке изображены тетраэдр, гексаэдр, октаэдр, додекаэдр и икосаэдр. Их форма – образец совершенства! А почему правильные многогранники получили именно такое название? Какими особенностями они обладают? Как изготовить модель какого-либо правильного многогранника? Где можно встретить эти удивительные тела?
Ответить на эти и другие вопросы: цель данной работы.
Основные понятия.
-
Многогранник – это геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями.
Стороны граней – рёбра многогранника, а концы рёбер – вершины многогранника. По числу граней различают четырёхгранники, пятигранники и т. д.
-
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости , каждой из его граней.
-
Выпуклый многогранник называется правильным, если все его грани – одинаковые правильные многоугольники, в каждой вершине сходится одно и то же число рёбер, а соседние грани образуют равные углы.
Все правильные многогранники имеют разное число граней и названия получили по этому числу.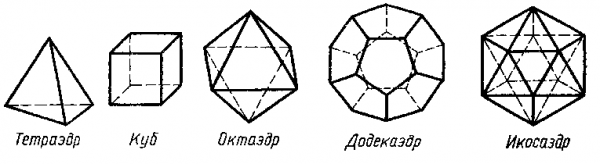
-
Тетраэдр ( от ,,тетра”– четыре и греческого ,,hedra” – грань) составлен из 4-х правильных треугольников, в каждой его вершине сходятся 3 ребра.
-
Гексаэдр ( от греческого ,,гекса” – шесть и ,,hedra” – грань) имеет 6 квадратных граней, в каждой его вершине сходятся 3 ребра.
12 стр., 5908 словСовременная игрушка в жизни ребенка
... проанализировать методическую и теоретическую литературу по проблеме исследования, выявить основные особенности современной игрушки и значение игрушки для ребенка. Для достижения поставленной цели необходимо решить следующие задачи: 1. Проанализировать методическую и ...
Гексаэдр больше известен как куб (от латинского ,, cubus” ; от греческого ,,kubos”.
-
Октаэдр ( от греческого okto – восемь и hedra – грань) имеет 8 граней (треугольных), в каждой вершине сходятся 4 ребра.
-
Додекаэдр ( от греческого dodeka – двенадцать и hedra – грань) имеет 12 граней ( пятиугольных), в каждой вершине сходятся 3 ребра.
-
Икосаэдр (от греческого eikosi – двадцать и hedra – грань) имеет 20 граней (треугольных), в каждой вершине сходится 5 рёбер. (5, с.267-269)
Оказывается, что правильных многогранников ровно пять — ни больше ни меньше. Ведь для того, чтобы получить какой-нибудь правильный многогранник, в каждой вершине, согласно его определению, должно сходиться одинаковое количество граней, каждая из которых является правильным многоугольником.
Сумма плоских углов многогранного угла должна быть меньше 360 о , иначе никакой многогранной поверхности не получится. Перебирая возможные целые решения неравенств: 60к < 360, 90к < 360 и 108к < 360 (к — число плоских углов, сходящихся в одной вершине многогранника).
доказывается, что правильных многогранников ровно пять. (2)
Исторические сведения о правильных многогранниках.
Древнегреческий философ Платон, (428 или 427 до н. э. — 348 или 347), проводивший беседы со своими учениками в роще Академа (Академ – древнегреческий мифологический герой, которого, по преданию, похоронили в священной роще недалеко от Афин, откуда и пошло название ,,академия”), одним из девизов своей школы провозгласил: ,, Не знающие геометрии не допускаются!”
Правильные многогранники называют также Платоновыми телами. Хотя их знаки пифагорейцы за несколько веков до Платона.
В диалоге ,,Тимей’’ он связал правильные многогранники с четырьмя основными стихиями. Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх; икосаэдр — воду, т.к. он самый «обтекаемый»; куб — землю, как самый «устойчивый»; октаэдр — воздух, как самый «воздушный». Пятый многогранник, додекаэдр, воплощал в себе «все сущее», символизировал все мироздание, считался главным. Хотя правильные многогранники были известны пифагорейцам за несколько веков до Платона, их называют платоновыми телами. (4, с.340)
Важное место занимали правильные многогранники в системе гармоничного устройства мира И. Кеплера.(2)
Изготовление моделей правильных многогранников.
Однажды обычный английский мальчик Джеймс, увлёкшись изготовлением моделей многогранников, написал в письме к отцу: ,, … Я сделал тетраэдр, додекаэдр и ещё два эдра, для которых не знаю правильного названия”. Эти слова знаменовали рождение в пока не примечательном мальчике великого физика Джеймса Кларка Максвелла. Думается, что и вас, и ваших родных увлечёт изготовление моделей геометрических тел. ( 4, с.23)
Если поверхность многогранника разрезать по некоторым рёбрам, а затем развернуть её на плоскости, то получится фигура, которую называют развёрткой многогранника. На следующем рисунке показано, как можно получить развёртку куба.
В зависимости от того, по каким рёбрам сделаны разрезы, развёртки могут быть разными.
При изготовлении моделей многогранников были использованы следующие развёртки.
Формирование правильной осанки
... культурой и спортом - самое лучшее средство предупреждения нарушений осанки. Воспитание правильной осанки можно сравнить с выработкой особого вида условного двигательного рефлекса, ... спереди напоминает букву “С”. Она может быть обращена вершиной в правую или левую сторону. У детей до ... сидеть, а для этого надо подобрать мебель, подходящую по росту. Проверить это просто: крышка стола должна быть ...

Есть ещё один способ изготовления многогранников, при котором они сплетаются из нескольких полосок бумаги. Без применения клея модель приобретает жёсткую структуру после того, как будет заправлен последний кусочек бумаги.
Например, тетраэдр можно сплести из двух полосок состоящих из четырёх равных правильных треугольников.


-
Согнём и разогнём каждую из полосок по пунктирным линиям, чтобы образовались сгибы.
-
Наложим тёмную полоску на белую, как показано на рисунке.







-
Сложим из белой полоски тетраэдр.
-
Обернём тёмной полоской 2 грани тетраэдра и оставшийся треугольник вставим в щель между двумя белыми треугольниками.


Куб можно сплести из 3-х полосок, разделённых на 5 квадратов.
1)Вырежем 3 такие полоски (белую, жёлтую и красную).

2)Сложим белую полоску так, как показано на рисунке.
3)Обернём её жёлтой полоской.
4)Получим куб, у которого передняя и задняя грани белые, а остальные жёлтые.
5)Третью полоску (красную) пропустим сзади куба в щель между белой и жёлтой полосками, согнём и конечные квадраты также пропустим в щель между передней белой гранью и жёлтой полоской.
Из 3-х полосок разного цвета получается куб, у которого противоположные грани одинакового цвета. ( 3, с.41-44)
Формула Эйлера.
-
Подсчитаем число вершин (В), граней (Г), рёбер (Р) запишем результаты в таблицу.
|
Многогранник |
Вершины |
Грани |
Рёбра |
В+Г-Р |
|
Тетраэдр |
4 |
4 |
6 |
2 |
|
Гексаэдр |
8 |
6 |
12 |
2 |
|
Октаэдр |
6 |
8 |
12 |
2 |
|
Додекаэдр |
20 |
12 |
30 |
2 |
|
Икосаэдр |
12 |
20 |
30 |
2 |
В последней колонке для всех многогранников один и тот же результат: В+Г- Р=2. Доказал это удивительное соотношение один из величайших математиков Леонард Эйлер (1707 – 1783), поэтому формула названа его именем: формула Эйлера. Этот гениальный учёный, родившийся в Швейцарии, почти всю жизнь прожил в России, и мы с полным основанием и гордостью можем считать его соотечественником.
Самое удивительное в этой формуле, что она верна не только для правильных многогранников, но и для всех многогранников!
Ради интереса можно проверить это для нескольких наугад взятых многогранников. (3, с.42)
|
Объект |
Форма |
Вершины |
Грани |
Рёбра |
В+Г-Р |
|
Пирамида Хеопса |
Четырёхугольная пирамида |
5 |
5 |
8 |
5+5-8=2 |
|
Здание лицея №1 г.Кунгура |
Прямая призма(прямоугольный параллелепипед) |
8 |
6 |
12 |
8+6-12=2 |
Например
,,Закон взаимности” для Платоновых тел.
У правильных многогранников есть интересная особенность – своеобразный ,,закон взаимности”. Центры граней куба являются вершинами октаэдра, а центры граней октаэдра – вершинами куба.
Центры граней додекаэдра являются вершинами икосаэдра, а центры граней икосаэдра – вершинами додекаэдра.
Особняком от этих 4-х многогранников стоит тетраэдр: если считать центры его граней вершинами нового многогранника, то вновь получится тетраэдр.
Куб и октаэдр, додекаэдр и икосаэдр – это две пары двойственных многогранников. У них одинаковое число рёбер (12 – у куба и октаэдра; 30 – у додекаэдра и икосаэдра), а числа вершин и граней переставлены.
Тетраэдр двойствен сам себе.(5)
Правильные многогранники вокруг нас.
В книге немецкого биолога начала нашего века Э. Геккеля «Красота форм в природе» можно прочитать такие строки: «Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы». Так, например, одноклеточные организмы феодарии, имеют форму икосаэдра.
Интересно и то, что именно икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень — икосаэдр. Его геометрические свойства, о которых говорилось выше, позволяют экономить генетическую информацию. Правильные многогранники — самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли NaCl, монокристалл алюминиево-калиевых квасцов имеет форму октаэдра, кристалл сернистого колчедана FeS имеет форму додекаэдра, сурьменистый сернокислый натрий — тетраэдра, бор — икосаэдра.
Интересная научная гипотеза, авторами которой (в начале 80-х годов) явились московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли, проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Их 62 вершины и середины ребер, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления.
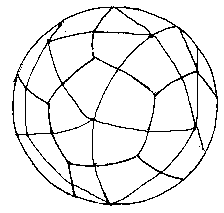
Если нанести на глобус очаги наиболее крупных и примечательных культур и цивилизаций Древнего мира, можно заметить закономерность в их расположении относительно географических полюсов и экватора планеты. Многие залежи полезных ископаемых тянутся вдоль икосаэдрово-додекаэдровой сетки. Еще более удивительные вещи происходят в местах пересечения этих ребер: тут располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, здесь шотландское озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой красивой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место. (2, с.2)
Заключение.
Исследовательская работа была интересной и разнообразной и заставила понять, что мир, окружающий нас, подчиняется законам геометрии.
В рамках работы над рефератом была изучена литература по теме, выявлены особенности правильных многогранников, изготовлены чертежи, развёртки, модели правильных многогранников.
Теория многогранников – один из увлекательных и ярких разделов математики. В представленном реферате была рассмотрена только одна часть этой теории. Из правильных многогранников – платоновых тел – можно получить так называемые полуправильные многогранники, или архимедовы тела (их 13), гранями которых являются также правильные, но разноимённые многоугольники, а также звёздные правильные тела (их 4).
Изучение этих многогранников может стать содержанием нового реферата.
Библиография.
[Электронный ресурс]//URL: https://psychoexpert.ru/referat/pravilnyie-mnogogranniki-v-filosofskoy-kartine-mira-platona/
1.Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Часть 3 – М: Баласс, 1988.
2.www.5ballov.ru
3.Шарыгин И. Ф., Ерганжиева Л.Н. Наглядная геометрия.Учебное пособие для V – VI классов. – М: Мирос 1992.
4.Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.
5.Энциклопедия для детей. Я познаю мир.Математика. – М: Издательство АСТ, 1999.
