Формирование понятия ‘множество’ у детей младшего школьного возраста

метки: Множество, Ребенок, Развитие, Представление, Объект, Предмет, Понятие, Элемент

Сейчас век стремительно развивающихся технологий. Человеку необходимо всё больше знаний для его разностороннего развития.

Ежедневно в жизни: дома, на улице ребёнок начинает встречаться с такими ситуациями, где он принимает, хоть и элементарное, но все же математического решение. Он демонстрирует знания таких отношений, как много-мало, больше-меньше-поровну, умения определить количество предметов во множестве, выбрать соответствующее количество элементов из множества и т. д. Возникающие проблемы дети решают сначала при помощи взрослых, а затем самостоятельно.

Качественное овладение учениками основами математических представлений оказывает положительное влияние на весь ход их психического развития, что доказывают современные психолого-педагогические исследования.

До второй половины XIX века понятие ―множество‖ не рассматривалось в качестве математического (―множество книг на полке‖, ―множество человеческих добродетелей‖ и т. д. — всё это чисто бытовые обороты речи).

Положение изменилось, когда немецкий математик Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным ―множеством‖ или элементом множества. Можно сказать, что множество — это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимы друг от друга. Примерами множеств могут быть: множество овощей (картофель, капуста, морковь, огурцы, помидоры, свекла), множество деревьев (берёза, осина, сосна, дуб, ель, липа, тополь), множество животных (лошадь, кошка, осёл, волк, заяц), а также множество N натуральных чисел 1, 2, 3, …, множество Р простых чисел 2, 3, 5, 7, 11. Множество, не содержащее элементов, называется пустым.

В начальной школе есть несколько программ, в которых предусмотрено изучение понятия «множество» и его свойств. Авторы соответствующих учебников: Петерсон Л. Г (Образовательная программа школа 2000); Демидова Т.Е., Козлова С.А., Тонких А.П (Образовательная программа школа 2100); Горячев А.В.

При работе над выпускной квалификационной работой я изучила учебники указанных авторов, а также научно-методическую литературу таких авторов как: Звонкин А.К., Столяр А.А., Локшин А.А., Иванова Е.А. посвящённую формированию понятия множества. В процессе исследования я выяснила, что, несмотря на кажущуюся простоту понятия «множество», детям не всегда легко усвоить основные знания, относящиеся к понятию» множество» и его свойствам.

Повышение эффективности социальных программ. Показатели оценки ...

... часто употребляемым понятием и постоянно используемым в практике государственного управления, социальное программирование не подразумевает пока обязательной комплексной оценки эффективности на всех стадиях разработки его продукта - «социальных программ». В связи ...

Многие психологи в своих исследованиях отмечали, что наглядные средства обучения должны точно отражать характерные признаки и свойства объектов, которые изучаются в данный момент, а все остальное, несущественное (излишняя детализация) отвлекает внимание детей. Значительный вклад в понимание природы восприятия внесли психологи и педагоги — А.В. Запорожец, В.П. Зинченко, А.Н. Леонтьев, Л.А. Венгер, Л.С. Выготский, Б.Г. Ананьев и др.

Именно поэтому необходимо использовать самые разнообразные методики, повышающие эффективность усвоения понятия. Я предположила, что большую помощь в формировании понятия «множество» могут оказать современные мультимедийные технологии: использование интерактивных досок (смарт досок), MacBook.

Одно из наиболее часто используемых на уроках технических устройств это интерактивная доска. Возможности интерактивной доски практически безграничны, преимущества её использования состоят в том, что она позволяет в интерактивном режиме показывать детям какой-либо процесс. В частности, учащиеся могут наглядно на интерактивной доске увидеть как сами множества, так и производить операции объединения и пересечения множеств. При этом учитель имеет возможность передвигать, накладывать друг на друга, удалять или добавлять новые объекты. Интерактивная доска расширяет возможности презентации. Учитель может во время показа слайдов подчёркивать значимое, выделять цветом или другим образом то, на что надо обратить внимание детей. При закреплении нового понятия использование интерактивной доски позволит детям увидеть свои ошибки и исправить их сразу же.

Опираясь на вышеизложенное, можно утверждать, что выбранная нами тема является актуальной в настоящее время.

Цель работы: выявить способы формирования представлений о множестве у детей младшего школьного возраста

Объект исследования — процесс формирования представления о множестве

Предмет исследования — формирование у детей младшего школьного возраста представлений о множестве различными способами.

Для достижения цели работы я сформулировала следующие задачи.

Задачи работы:

1. Изучить понятия о множестве в учебной литературе детей младшего школьного возраста.

2. Изучить возрастные особенности детей младшего школьного возраста.

3. Выявить возможности использования мультимедийных технологий в формировании представлений о множестве.

4. Выявить отношение детей к урокам с использованием компьютерных обучающих программ (на основе анкетирования).

5. Разработать дидактический материал для работы с детьми по теме «множество».

ГЛАВА 1. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ФОРМИРОВАНИЯ ПОНЯТИЯ О МНОЖЕСТВЕ У ДЕТЕЙ МЛАДШЕГО ШКОЛЬНОГО ВОЗРАСТА

1.1 Возрастные особенности развития детей младшего школьного возраста

Переход в школьный возраст связан с решительными изменениями в его деятельности, общении, отношениях с другими людьми. Ведущей деятельностью становится мышление и учение, изменяется уклад жизни, появляются новые обязанности, новыми становятся и отношения ребенка с окружающими.

Поступивший в школу ребенок автоматически занимает совершенно новое место в системе отношений людей: у него появляются постоянные обязанности, связанные с учебной деятельностью. Близкие взрослые, учитель, даже посторонние люди общаются с ребенком не только как с уникальным человеком, но и как с человеком, взявшим на себя обязательство (неважно — вольно или по принуждению) учиться, как все дети в его возрасте.

Физиологические особенности детей младшего школьного возраста

... Ваши дети младшего школьного возраста успеют освоить всю необходимую программу и сохранить здоровье и интерес к учебе. Каковы же важные физиологические особенности младшего школьного возраста? Рассмотрим более детально. 1. Глобальная перестройка организма Младший школьный возраст - время ...

Происходит переход от наглядно — образного к словесно — логическому мышлению. У ребёнка появляются логически верные рассуждения: он использует операции. Однако это ещё не формально — логические операции, рассуждать в гипотетическом плане младший школьник ещё не может. Операции, характерные для данного возраста, Ж. Пиаже назвал конкретными, поскольку они могут применяться только на конкретном, наглядном материале. В процессе обучения у младших школьников формируются научные понятия. Оказывая крайне важное влияние на становление словесно — логического мышления, они, тем не менее, не возникают на пустом месте. Для того, чтобы их усвоить, дети должны иметь достаточно развитые житейские понятия — представления, приобретённые в дошкольном возрасте и продолжающие спонтанно появляться вне стен школы на основе собственного опыта каждого ребёнка. Житейские понятия — это нижний понятийный уровень, научные — верхний, высший, отличающийся осознанностью и произвольностью. По выражению Л. С. Выготского, «житейские понятия прорастают вверх через научные, научные понятия прорастают вниз через житейские». Овладевая логикой науки, ребёнок устанавливает соотношения между понятиями, осознаёт содержание обобщённых понятий, а это содержание, связываясь с житейским опытом ребёнка, как бы вбирает его в себя. Научное понятие в процессе усвоения проходит путь от обобщения к конкретным объектам.

Овладение в процессе обучения системой научных понятий даёт возможность говорить о развитии у младших школьников основ понятийного, или теоретического, мышления. Это мышление позволяет ученику решать задачи, ориентируясь не на внешние, наглядные признаки и связи объектов, а на внутренние, существенные свойства и отношения. Развитие теоретического мышления зависит от типа обучения.

Наряду с усвоением содержания системы научных понятий ребёнок овладевает способами организации нового для него вида труда — учебного. В этот момент появляется качественно новое свойство человеческой психики — рефлексия. Она проявляется в возможности выделять особенности своих действий и делать их предметом анализа. Уже к четвёртому классу ребёнок может сам поставить перед собой учебную задачу, составить режим работы, оценить и проверить её.

Как говорил В. А. Сухомлинский: «Учение становиться трудом только при условии, когда в нём есть важнейшие признаки всякого труда — цель, усилия, результаты». И тогда результатом учебного труда является научное мышление.

Развитие других психических функций зависит от развития мышления. В начале младшего школьного возраста восприятие недостаточно дифференцировано. Из-за этого ребёнок иногда путает похожие по написанию буквы и цифры. Хотя он может целенаправленно рассматривать предметы и рисунки, им выделяются так же, как и в дошкольном возрасте, наиболее яркие, бросающиеся в глаза свойства — в основном, цвет, форма, величина.

К концу младшего школьного возраста, при соответствующем обучении, появляется синтезирующее восприятие. Развивающийся интеллект создаёт возможность устанавливать связи между элементами воспринимаемого.

Несмотря на то, что в этот период большое значение имеет наглядно — образное мышление, непосредственно воспринимаемое ребёнком, уже не мешает ему рассуждать и делать правильные выводы. Как известно, в 7 — 8 лет исчезают феномены Пиаже. И теперь интеллектуальные операции позволяют ребёнку судить о вещах без жёсткой зависимости от наглядной ситуации.

Особенности детей младенческого возраста

... возрасте и их влияние на младенца. 1. Кризис новорожденности Первый год жизни ребенка можно разделить на два периода: новорожденности и младенчества. Периодом новорожденности ... яркая освещенность, необходимость смены питания); психологические. Отделяясь от матери, ребенок перестает ощущать ... существования в чреве матери. Младенчество - период, когда ребёнок развивается в физическом, психическом и ...

Память развивается в двух направлениях — произвольности и осмысленности. Младшие школьники способны целенаправленно, произвольно запоминать материал, им не интересный.

Младшие школьники обладают хорошей механической памятью. Они склонны дословно воспроизводить то, что запомнили. Совершенствование смысловой памяти в этом возрасте даёт возможность освоить достаточно широкий круг мнемонических приёмов, т.е. рациональных способов запоминания. Когда ребёнок осмысливает учебный материал, понимает его, он его одновременно и запоминает. Таким образом, интеллектуальная работа является в то же время мнемонической деятельностью, мышление и смысловая память оказываются неразрывно связанными.

В младшем школьном возрасте развивается внимание. Без достаточной сформированности этой психической функции процесс обучения невозможен.

Младшие школьники уже способны концентрировать внимание на неинтересных действиях, но у них всё ещё преобладает непроизвольное внимание. Для них внешние впечатления — сильный отвлекающий фактор, им трудно сосредоточиться на непонятном, сложном материале. В этом возрасте внимание имеет ряд недостатков, таких как:

• узкое внимание (ребёнок не в состоянии наблюдать одновременно много предметов, и его внимание всецело поглощается тем немногим, что в данный момент занимает его);
• легко утомляемое внимание (ребёнок не может долго сосредоточить внимание, особенно на одном и том же);
• блуждающее внимание (школьнику трудно установить внимание, уверенно, твёрдо и правильно фиксировать его);
• пассивное внимание (детское внимание малоспособно к произвольному усилию и нуждается в частых побуждениях);
• конкретное внимание (направляется преимущественно на предметы внешнего восприятия).

В учебной деятельности развивается произвольное внимание ребёнка. Первоначально следуя указаниям учителя, работая под его постоянным контролем, он постепенно приобретает умение выполнять задания самостоятельно — сам ставит цель и контролирует свои действия. Контроль за процессом своей деятельности и есть, собственно, произвольное внимание ученика.

Разные дети внимательны по-разному: внимание обладает разными свойствами, и эти свойства развиваются у них в неодинаковой степени, создавая индивидуальные варианты. Одни ученики имеют устойчивое внимание, но плохо переключаемое внимание, они довольно долго и старательно решают одну задачу, но быстро перейти к следующей им трудно. Другие легко переключаются в процессе учебной работы, но также легко отвлекаются на посторонние моменты. У третьих хорошая организация внимания сочетается с его малым объёмом.

В целом можно выделить две основные линии развития психических функций — интеллектуализацию и произвольность.

1.2 Проблема формирования понятия о множестве у детей младшего школьного возраста в научной литературе

Ежедневно в нашей жизни: дома, на улице ребёнок начинает встречаться с такими ситуациями, где он принимает, хоть и элементарное, но все же математического решение. Он демонстрирует знания таких отношений, как много-мало, больше-меньше-поровну, умения найти количество объектов во множестве, выбрать соответствующее количество элементов из множества и т. д. Возникающие проблемы дети решают сначала при помощи взрослых, а затем самостоятельно.

Понятие измерения в психологии. Измерительные шкалы

... множества реакций, строится и соответствующая шкала измерения. По общепринятой классификации для субъективных измерений обычно рассматривают четыре основных типа шкал Рассмотрим особенности психологических измерений более подробно. Значение психологических измерений ... 1. Специфика психологических измерений 1.1 Понятие измерения в психологии Самые первые методы психологических измерений были ...

Качественное овладение учениками математических представлений, оказывает хорошее влияние на весь ход их психического развития, что доказывают современные психолого-педагогические исследования.

Многие учёные, среди которых Л.С. Выготский, Ж. Пиаже, Д.Б. Эльконин, В.В. Давыдов, П.Я. Гальперин, Л.И. Айдарова и другие занимались исследовательской работой, посвященной формированию математических понятий у детей.

До второй половины XIX века понятие ―множество‖ не рассматривалось в качестве математического (―множество книг на полке‖, ―множество человеческих добродетелей‖ и т. д. — всё это чисто бытовые обороты речи).

Положение изменилось, когда немецкий математик Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным ―множеством‖.

Можно сказать, что множество — это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимые друг от друга. Примерами множеств могут быть: множество овощей (картофель, капуста, морковь, огурцы, помидоры, свекла), множество деревьев (берёза, осина, сосна, дуб, ель, липа, тополь), множество животных (лошадь, кошка, осёл, волк, заяц), а также множество N натуральных чисел 1, 2, 3, …, множество Р простых чисел 2, 3, 5, 7, 11. Множество, не содержащее элементов, называется пустым.

При изучении учащимися начальной школы понятия множества возникают определенные трудности. Например, детям непросто понять, что такое равные множества. Отсюда появляются трудности с пониманием смысла таких операций как объединение и пересечение множеств, причем эти трудности присутствуют не только у школьников, но даже у студентов. Источник этих затруднений заключается в смешении двух фундаментальных понятий — одинаковый и тот же.

Вот что пишут о данной проблеме А.А. Локшин и Е.А Иванова в работе [28].

«В работе [40] вполне убедительно продемонстрировано, что уже 5 — 6 летние дети успешно справляются с классификацией предметов по двум признакам, т.е. фактически работают с диаграммами Эйлера. Может быть, непонимание сути понятия «равные множества» связано не с тем, что психика младших школьников ещё недостаточно созрела для восприятия такого сложного понятия, как «множество», а в том, что взрослые по умолчанию предлагают некоторые соглашения выполненными, в то время как детям их нужно объяснять?

Приведём определения из учебника Л.Г. Петерсон: «Два множества равны, если они состоят из одних и тех же элементов. Если множество А и В равны, то пишут А = В. Путь А= {малина, земляника, смородина}, В= {земляника, малина, смородина}. А = В (в них одни и те же элементы, только в разном порядке)». После такого объяснения на уроке может возникнуть осложнение, о котором авторам сообщил доктор педагогических наук профессор А.Л. Чекин. В качестве примера рассмотрим рисунок 1, на котором схематически изображен шкаф с двумя полками.

Педагогическая система, ее элементы и их взаимосвязь

... явление, как педагогическая система. Разные авторы дают следующие формулировки понятия «система»: 1) множество взаимосвязанных компонентов, составляющих определенное целое в своем строении и функционировании. (С.И. Архангельский). 2) определенная общность элементов, функционирующих ...

На верхней полке стоят три банки варенья (например, вишнёвое, клубничное, земляничное).

На нижней полке находятся такие же три банки, но в другом порядке. Совокупность трёх верхних банок обозначается на рисунке А, а совокупность трёх нижних банок- В. Учитель спрашивает ученика: «Равны ли множества А и В?». Ученик отвечает: «Да, равны».

Итак, мы столкнулись с серьёзной проблемой: как объяснить ученику, что множества А и В не равны, если, глядя на подчёркнутые выше строчки из определения равных множеств А и В, он не заметит никакой разницы между определением равных множеств и рис. 1. Отличие, очевидно, заключается в том, что в приведённом выше определении в фигурных скобках перечислены имена объектов, а сами объекты (элементы множества) подразумеваются. Что же это за подразумеваемые объекты? В рассматриваемом случае это понятия, обозначаемые соответствующими словами. В то же время на рис. 1 присутствуют не имена объектов, а, напротив, сами объекты. Таким образом, работая с множествами, нам предстоит иметь дело с двумя разными ситуациями.

Ситуация 1. В фигурных скобках перечисляются имена объектов (элементов множества).

Ситуация 2. На рисунке присутствуют сами объекты (элементы множества).

Рассмотрим особенности каждой ситуации.

В ходе анализа ситуации 1 важно обратить внимание на два условия.

Условие 1. В перечислении, записываемом в фигурных скобках, ни в коем случае не должны участвовать сами элементы, а должны присутствовать только их имена.

Условие 2. Из контекста должно быть ясно, каким объектам соответствует перечисленное в фигурных скобках имена. Тогда недоразумения, связанные с «проблемой равных множеств», не возникнут.

Из сказанного выше вытекает, что нам следует согласиться, например, со следующими равенствами множеств, заданных перечислением: {I, II, III, IV, V}={1, 2, 3, 4, 5}; {клубника, малина}={МАЛИНА, КЛУБНИКА}.

При этом перечисление, аналогичное изображению на рис. 2, недопустимо вследствие его двусмысленности.

Конечно, можно специально договориться, что животное на рис. 2 — это имя какого-то объекта (а не сам объект).

Однако лучше этого избежать и пользоваться для производства имен известными стандартными алфавитами.

В ходе анализа ситуации 2 также важно обратить внимание на два условия.

Условие 1. Как известно, в макромире не бывает абсолютно одинаковых объектов. Это обстоятельство необходимо всячески подчеркивать, а не затушевывать! Если бы банки с вареньем, изображенные на рис. 1, имели хотя бы самые незначительные индивидуальные признаки, ученик не мог бы ошибиться. Таким образом, объекты, присутствующие на рисунке, обязательно должны обладать индивидуальными признаками. Соблюдение этого условия исключит путаницу, при которой два разных множества принимаются за равные.

Условие 2. Соблюдение договоренности о способах многократного изображения одного и того же предмета (множества предметов).

Остается ещё не разобранным случай, когда нужно дважды (трижды, четырежды…) изобразить одно и тоже множество. Например, показать на рисунке, что множество из трёх банок варенья не изменится (останется равным самому себе), если мы поменяем две банки местами. Этого не трудно добиться, например, таким способом: поместив на рисунок «живого персонажа, переставляющего банки».

Перечисленные выше проблемы введения понятия «равные множества» связаны с различением понятий «такой же» и «тот же самый». Если младшие школьники работают с карточками, которые (в отличие от рисунков на странице учебника) можно перекладывать, то эти проблемы, как правило, исчезают. Заметим в этой связи, что упомянутый выше «живой персонаж» не может быть «таким же», он обязательно «тот же самый». Если ребёнок играет с объемным материальным предметом, который он может трогать, наблюдать за ним, то путаницы между понятиями «такой же» и «тот же самый» не возникает. (К примеру: это тот же самый мячик, с которым сейчас играл ребёнок, или похожий мячик, но не тот же самый.) Но если школьнику приходится работать не с самими объектами, а их изображениями (на странице в учебнике, на мониторе компьютера), то, если не принять специальных мер предосторожности, путаница неизбежна. Возникает две ситуации: дважды изображен один и тот же объект, или изображены два одинаковых предмета.

А.К Звонкин в книге «Малыши и математика» отмечает, что ребятам очень трудно даются задачи на пересечение классов. Вся сложность в том, что ребенок должен логически рассуждать при выполнении подобных заданий, например, таких: даны пять картинок (резиновые сапоги, шапка, мяч, автомобильная шина, пальто) и их нужно разбить на две группы. Ребенок должен прийти к выводу, что (резиновые сапоги, мяч, автомобильная шина) — это предметы, сделанные из резины. (Пальто, шапка, сапоги) — это предметы одежды. Сапоги мы отнесли как к первой, так и ко второй группе, потому что это обувь, которая сделана из резины — значит это общий элемент. Теперь возникает вопрос: как поделить эту картинку, не порвав ее пополам? Звонкин А.К. предлагает воспользоваться приемом веревочных кругов, в пересечении которых нужно поместить общий объект. (рис.1) На рисунке изображены два множества, в каждом из которых 3 объекта. Сапоги являются «общим объектом». Математики говорят: «лежат в пересечении» этих множеств.

А.К. Звонкин предлагает проводить все свои занятия в игровой форме. Это помогает ребятам лучше усваивать материал. Много заданий посвящены теме пересечения и объединения множеств. Звонкин предлагает детям находить разные предметы, сравнивать их. «Где нарисованы те предметы, которые есть на картинке А и которых нет на картинке В, а где предметы, которые есть и на той, и на другой картинке?» Он смотрит, как ребята работают с материалом, как они приходят к тем или иным выводам. Часто в начале занятия дети не понимают задания, кладут предметы не в те места, спорят, отнимают друг у друга карточки, но это проходит и вскоре находится правильное решение, которые дети тщательно проверяют.

А.А. Столяр в своей книге «Формирование элементарных математических представлений у дошкольников» рассказывает, что уже в детстве ребенок накапливает знания о разных предметах и объектах. Уже на первом — втором году жизни ребенок играет с различными объектами, такими как: шарики, мячики, кольца и так далее. Он перебирает, складывает -раскладывает, группирует предметы, по форме, размеру, цвету. Дети знакомятся с таким понятием как множество на собственном опыте: множество людей, множество зверей в зоопарке — все это воспринимается слуховыми, зрительными анализаторами. Ребенок различает, где один, а где несколько объектов, как одно множество отличается от другого, сравнивают множества по количеству элементов. Ребята группируют множества. К примеру, из пуговиц большого и маленького размера можно получить два множества. А. А. Столяр считает, что формирование понятия «множество» успешно при наглядно-действенной форме обучения.

1.3 Проблема формирования понятия о множестве у детей младшего школьного возраста в учебной литературе

В начальной школе есть несколько программ, в которых предусмотрено изучение понятия «множество» и его свойств. Например, это учебники авторов: Петерсон Л. Г (Образовательная программа — школа 2000); Демидова Т.Е., Козлова С.А., Тонких А. П. (Образовательная программа — школа 2100); Горячев А.В.

Я изучила учебники указанных авторов, а также научно-методическую литературу, посвящённую формированию понятия множество, и сформулировала для себя следующие выводы:

в учебнике Информатики за 3 класс, Горячева А.В. даётся адаптированное под возраст младшего школьника определение понятия множества: «Множество — это группы одинаковых объектов». Так же наглядным путём объясняется понятие «элементы множества». Само понятие «множество» вводится уже в третьей четверти 1 класса. Александр Владимирович начинает знакомство от простого к сложному. Он объясняет, что все предметы и явления можно объединять в группы, и такие группы в математике и информатике называют множествами. Для объединения во множество достаточно выделить характерный признак, по которому можно четко определить принадлежность к нему предмета. (Пример: множество людей, игрушек, животных).

Другой же предмет, у которого этот признак отсутствует, включать в элементы этого множества нельзя (множество людей только в синей одежде, множество только мягких игрушек, множество только домашних животных).

Уроки хорошо продуманы. Каждое задание красочно оформлено, что привлекает внимание младшего школьника.

В учебнике «Математика, 3 класс», Петерсон Л.Г. даётся немного другое понятие множества: «Когда какие — нибудь объекты собирают вместе, в математике используют для их названия общее слово — множество». Людмила Георгиевна рассказывает ребятам, что мы не можем сказать «стадо чашек», а множество чашек — можем. Учебник учит ребят не только называть множества, находить его элементы, находить пустые множества, но и правильно выстраивать предложения. Петерсон Л.Г. даёт следующее определение элементам множества: «Предметы и живые существа, входящие в множество, называют элементами этого множества. Например, ласточка — это элемент множества птиц, берёза — это элемент множества деревьев. В тоже время хвост ласточки не является элементом множества птиц, а лист берёзы или подберёзовик не являются элементами множества деревьев». Ребят учат задавать множества. «Множество задано, если определены его элементы, то есть о любом объекте можно точно сказать, является ли он элементом этого множества или нет. Множество иногда задают перечислением его элементов. Например, множество букв в слове «шар» состоит из трёх элементов: ш, а, р. Элементы множества записывают в фигурных скобках: {ш, а, р}. Если во множестве много элементов, то их трудно или даже невозможно перечислить. Например, множество рыб в океане, множество домов в Москве. Такое множество можно задать общим свойством его элементов. Множество обозначают заглавной буквой, например: К — множество учеников 3 «А» класса. Школьники знакомятся с такими понятиями, как равные множества и пустое множество. «Два множества равны, если они состоят из одних и тех же элементов. Если множества А и В равны, то пишут А = В, а если они не равны, то пишут А ≠ В. Пример: Пусть А = {малина; земляника; смородина}, В = {земляника; малина; смородина}, С = {смородина; малина; вишня}, D = {малина; земляника; смородина; крыжовник}. А = В (в них одни и те же элементы, только в разном порядке); А ≠ С (в А есть земляника, а в С вместо неё — вишня); А ≠ D (в D лишний элемент — крыжовник)» и «Если множество не содержит ни одного элемента, то говорят, что оно пустое. Пустое множество обозначается так: Ø.».

Людмила Георгиевна рассказывает ребятам о пересечении и объединении множеств «Пересечение множеств А и В — это их общая часть, то есть множество, состоящее из всех элементов, принадлежащих одновременно как А, так и В. Пересечение множеств обозначается знаком ∩. Операция пересечения множеств обладает переместительным и сочетательным свойствами. Переместительное свойство: А ∩ В = В ∩ А. Сочетательное свойство: (А∩В) ∩С = А ∩ (В∩С) Значит, результат пересечения множеств не зависит от порядка множеств и от порядка действий» и объединении «Все элементы множеств А и В, взятые вместе, образуют новое множество, называемое объединением множеств А и В. Объединение множеств обозначается символом ∪. Операция объединения множеств обладает переместительным и сочетательным свойствами. Переместительное свойство: А ∪ В = В ∪ А. Сочетательное свойство: (А∪В) ∪С = А ∪ (В∪С) Значит, результат объединения не зависит от порядка множеств и от порядка действий». А что же такое подмножество? «Множество А называют подмножеством множества В, если каждый элемент множества А является одновременно элементом В. Если А является подмножеством В, то между ними ставят знак ⊂, а если нет, то знак ⊂. Запись А⊂В читается: А является подмножеством В; А включено в В; А содержится в В. Соответственно, запись А ⊂ В читается: А не является подмножеством В; А не включено в В; А не содержится в В».

Учащиеся знакомятся и с таким понятием, как диаграмма Эйлера-Венна.

«Чтобы лучше представить себе множество, можно использовать рисунок, называемый диаграммой Эйлера-Венна. Это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи — элементы, не принадлежащие множеству. Например, диаграмму множества В = {2; m} можно нарисовать так: «Число 2 принадлежит множеству В, а буква А не принадлежит множеству В. 2∈В или А∉В»

После этого подобран интересный материал на отработку, осмысление и закрепление изученного понятия. К примеру: перечисли членов своей семьи

Принадлежишь ли ты этому множеству? А твой друг? Или перечисли множество девочек твоего класса, сидящих в первом, и т.д ряду.

Из всего вышесказанного я могу сделать вывод, что введенное понятие «множество» Петерсон Л. Г. достаточно доступно для детского понимания.

В учебнике «Математика, 3 класс» авторов Демидовой Т.Е., Козловой С.А., Тонких А.П знакомство с понятием «множество» происходит в середине учебного года. Ребята узнают новое, увидев проблемную ситуацию. На странице представлены три рисунка девочки (цветы, животные, игрушки), где сказано, что она не знает, как подписать эти рисунки и просит учеников придумать общее название для каждой группы предметов. После чего автор учебника вводит понятие множество: «В математике группу предметов или живых существ, собранных вместе, называют словом множество». Подход этого учебника построен на постановке сложных, поисковых ситуаций. Ребёнку нужно самостоятельно прийти тому или иному выводу. Школьникам встречаются задания такого типа: Костя написал на листах бумаги названия множеств и попросил Лику нарисовать по несколько элементов этих множеств. Кого или что могла нарисовать Лика? (деревья и насекомые) и т.д. На примере всё той же девочки Лики ребята знакомятся со способами задания множеств: «Вы видите все элементы множества «Предметы на столе Лики». Можно сказать, что художник перечислил все элементы этого множества. А значит, задал это множество перечислением. Теперь о любом предмете можно точно сказать, является он элементом этого множества или нет. Чтобы задать множество, можно назвать общее свойство всех его элементов. Например: цвет, материал, назначение. И тогда любой предмет, имеющий такое же свойство, будет элементом этого множества».

Мы считаем, что успешность формирования понятия множества у учащихся начальных классов можно повысить при помощи использования мультимедийных технологий на уроках.

Мультимедийные технологии — это совокупность современных средств аудио- теле-, визуальных и виртуальных коммуникаций, используемых в процессе организации, планирования и управления различных видов деятельности. Использование ИКТ в современной школе уже, скорее, необходимость, чем дополнительное средство. Рассмотрим вкратце, какие мультимедийные технологии могут быть использованы при формировании у детей понятия множества.

Наиболее часто на уроках используются мультимедийные презентации. При помощи ярких, красочных слайдов с добавлением музыки или двигающихся картинок, ссылок и переходов педагог может привлекать внимание детей даже к скучным для них понятиям. Изучая новое определение на слайде презентации, а не по учебнику, дети быстрее его запоминают, у них активизируется интерес к предмету и стремление узнавать новое. Презентации могут использованы для показа чертежей, графиков, таблиц и т.д.

Одно из наиболее часто используемых на уроках технических устройств, это интерактивная доска. Возможности интерактивной доски практически неограниченны, она позволяет в интерактивном режиме показать детям какой- либо процесс. При изучении понятия множества, учащиеся могут на интерактивной доске наглядно увидеть операции пересечения и объединения множеств. При этом учитель имеет возможность передвигать, накладывать друг на друга, удалять или добавлять новые объекты. Интерактивная доска расширяет возможности презентации, так как учитель может во время показа слайдов подчёркивать значимое, выделять цветом или другим образом то, на что надо обратить внимание детей. При закреплении нового понятия использование интерактивной доски позволит детям увидеть свои ошибки и исправить их сразу же. Контроль качества усвоения понятий проводят при помощи тестовых шаблонов, которых достаточно много в прилагаемом к доске программном обеспечении.

ГЛАВА 2. РОЛЬ МУЛЬТИМЕДИЙНЫХ ТЕХНОЛОГИЙ ПРИ ФОРМИРОВАНИИ ПРЕДСТАВЛЕНИЯ О МНОЖЕСТВЕ У ДЕТЕЙ МЛАДШЕГО ШКОЛЬНОГО ВОЗРАСТА

2.1 Выявление знаний у детей младшего школьного возраста о понятии «множество»

Опытно-практическая работа проводилась на базе ГБОУ СОШ № 868 города Москвы в период с 01 апреля по 30 апреля. Работа была проведена во 3 классе «А» (всего — 23 ребенка: 8 — мальчиков и 15 — девочек) и в 3 классе «Б» (всего — 22 ребенка: 10- мальчиков и 12 — девочек).

3 класс «А» — экспериментальная группа, 3 класс «Б» — контрольная группа. 3 класс «А» — ЭГ, 3 класс «Б» — КГ.

Наша экспериментальная работа состояла из трех этапов:

• первый — констатирующий этап

На этом этапе исследования детям были предложены анкета и таблицы, вопросы которых направлены на выявление знаний о понятие множество и на выявления отношения детей к изучению понятия множества перед началом опытно-практической работы.

• второй — формирующий этап

На данном этапе мы разработали и провели уроки: с контрольной группой проводились дидактические игры без использования мультимедийных технологий, с экспериментальной группой проводились дидактические игры с использованием мультимедийных технологий.

Нами были разработаны презентации к урокам, игры, направленные на формирование знаний детей о понятие множество.

• третий — контрольный этап

На этом этапе мы проводим повторную диагностику по ответам детей, провели анализ полученных результатов и выявили эффективность использования мультимедийных технологий на уроках.

На констатирующем этапе ставились следующие задачи:

1. Выявить отношения детей к изучению понятия множество.

2. Выявить знания младших школьников о понятие множество.

На констатирующем этапе, работа проводилась индивидуально с каждым ребенком.

Анкета

№ п/п	Вопросы	Ответы детей
1.	Почему тебе нравится изучать множества?	1.У меня это хорошо получается
		2.Мне нравятся такие уроки
		3.Я узнаю что-то новое
		4.Мне не интересно изучать множества
2.	Нужно ли уметь выделять множества?	1.Нужно
		2.Нет, не нужно
		3.Не знаю
3.	Для чего нужно уметь выделять элементы множества?	1.Многие предметы, окружающие нас, можно объединить в множества.
		2.Чтобы конструировать машины, строить дома.
		3. Чтобы быть умным.
		4.Не обязательно уметь выделять множества и элементы множества.
		5. Не знаю, взрослые говорят, что нужно.

Результаты ответов на анкету детей младшего школьного возраста на констатирующем этапе представлены в таблице 1.

Таблица 1 Таблица определения уровня знаний у детей на констатирующем этапе

№	Вопросы	Варианты ответов	ЭГ		КГ
			Кол-во ответов детей	Ответы в%	Кол-во ответов детей	Ответы в%
1	Почему тебе нравится изучать множеств а?	1.У меня это хорошо получается	4	17%	4	17 %
		2.Мне нравится такие уроки	4	17 %	4	17 %
		3.Я узнаю что-то новое	2	9 %	2	9 %
		4.Мне не интересно изучать множества	13	56 %	13	56 %
2	Нужно ли уметь выделять множеств а?	1.Нужно	10	35 %	10	35 %
		2.Нет, не нужно	6	22 %	6	22 %
		3.Не знаю	11	43 %	9	40 %
3	Для чего нужно уметь выделять элементы множеств а?	1.Многие предметы, окружающие нас, можно объединить в множества.	—	0 %	—	0 %
		2.Чтобы конструировать машины, строить дома.	4	17 %	5	22 %
		3. Что бы быть умным.	5	22 %	4	17 %
		4.Не обязательно уметь выделять множества и элементы множества.	3	13 %	3	13 %
		5.Не знаю, взрослые говорят, что это нужно.	11	48 %	11	48 %

младший школьный множество дидактический

При анализе ответов детей на анкету в контрольной и экспериментальной группах полученные данные отличались на 1-2 %

На 1 вопрос «Почему тебе нравится изучать множества?» 56,5%-57% ответили, что им не интересно изучать геометрические фигуры и 10 человек (43,5%) ответили на этот вопрос положительно.

На 2 вопрос «Нужно ли уметь выделять множества?» положительных ответов было 10, т.е. 10 человек (34,7%)

На 3 вопрос «Для чего нужно уметь выделять элемент множества?» 11 человек (47,8%) ответили, потому что так говорят взрослые.

Таким образом, исходя из выше приведенных данных, можно сделать вывод, что дети не понимают для чего им необходимо изучать множества и на уроках при изучении этой темы им не интересно.

Для выявления уровня знаний у детей о множестве было предложено следующее задание (Рис.1).

Для выявления уровня знаний у детей о множестве было предложены следующие задания. Детям предлагалось назвать множества, объяснить значение слова «множество».

На основании полученных данных можно сделать вывод, что 17человек (73,9%) правильно назвали множества и 13 человек (56,5%) верно сравнили множества.

Со вторым заданием, где детям предлагалось своими словами описать понятие множество, то как они понимают этот термин, справилось только 7 человек (30,4%).

Результаты опроса занесены в таблицы №1,2, на основании которых можно определить уровень знаний детей о множестве.

Рис.1 Задания для выявления уровня знаний у детей на констатирующем этапе (Задания разработаны на основе учебника Информатики за 3 класс, Горячева А.В.)

№	Задание:				Варианты ответа:
1	Впиши в таблицу названия множеств.				Четверг Среда Суббота Понедельник Пятница Воскресенье Вторник А Ё Ю У Я Ы 1 5 7 9 8 2 6 3 4 0
		Множества:
2	Нарисуй цветные круги в таблице.				Множества:
3
4	Сравни фотографии семьи Димы 5 лет назад, 1 год назад и теперь. Что можно сказать об этих множествах? Ответ:
5	Сравни множества по количеству элементов. (Поставь знаки «<», «>», «=». )
6	Сравни множества по количеству элементов. (Поставь знаки «<», «>», «=». )
7	Сравни множества по количеству элементов. (Поставь знаки «<», «>», «=». )

Уровень знаний детей о множестве на констатирующем этапе ЭГ

Таблица 1

№ п/п	Имя, фамилия	Номер задания							Понимание значения слова множество	Уровень знаний
		1	2	3	4	5	6	7
1	Арина Е.	—	+	—	+	—	+	+	+	В
2	Антон Г.	—	—	+	+	—	+	+	—	С
3	Артем С.	+	—	—	+	+	—	—	—	Н
4	Вера К.	—	—	+	+	+	+	—	+	В
5	Вероника Г.	+	—	—	—	+	—	+	—	Н
6	Вика С.	—	—	+	+	—	+	+	+	В
7	Даша М.	—	+	—	—	+	+	—	+	С
8	Егор К.	—	—	+	+	+	—	—	—	Н
9	Женя З.	+	—	—	—	+	—	—	Н
10	Катя А.	—	+	—	+	+	—	—	+	С
11	Коля С.	+	+	—	—	—	+	+	+	В
12	Лера Ж.	+	+	+	—	+	+	—	—	В
13	Лиза В.	+	+	—	+	—	+		—	С
14	Марьяна Г.	—	+	—	—	+	—	+	—	Н
15	Маша П.	—	—	+	+	—	+	—	+	С
16	Настя С.	—	—	+	—	+	—	+	—	Н
17	Самира Н.	+	—	—	+	—	+	—	+	С
18	Сережа К.	—	—	+	—	—	—	—	—	Н
19	Соня К.	—	—	—	+	—	+	+	+	С
20	Эмиль А.	—	—	—	+	+	+	—	—	Н
21	Юля У.	+	—	+	—	—	—	—	—	Н
22	Яна Я.	—	+	—	—	+	+	—	—	Н
23	Ярослав Б.	—	—	—	+	—	+	—	+	Н

Уровень знаний детей о множестве на констатирующем этапе КГ

Таблица 2

п/п	Имя, фамилия	Определение фигуры							Понимание значения слова множество	Уровень знаний
		1	2	3	4	5	6	7
1	Настя А.	+	—	—	+	+	+	—	—	С
2	Алевтина А.	—	—	+	+	—	+	+	—	С
3	Елена А.	+	—	+	+	—	—	—	—	Н
4	Дмитрий Б.	—	+	+	+	—	+	+	—	В
5	Софья Б.	+	+	—	+	—	—	—	—	С
6	Полина Б.	—	+	+	+	—	+	+	+	Н
7	Анна В.	+	+	—	+	+	—	—	—	С
8	Александр Г.	+	+	—	—	—	+	—	—	Н
9	Никита Г.	—	+	+	+	—	+	—	—	Н
10	Стефания Д.	+	+	+	+	—	—	+	+	С
11	Мария Е.	—	+	—	+	—	+	—	—	В
12	Стася И.	+	+	+	—	+	—	—	—	Н
13	Роман И.	—	+	—	—	+	+	—	—	Н
14	Мария К.	+	+	—	+	—	—	—	—	Н
15	Надежда К.	+	—	+	+	+	+	—	+	С
16	Никита К.	+	—	+	+	+	—	—	—	Н
17	Пётр Л.	+	+	+	—	+	—	+	С
18	Николай П.	+	+	+	+	—	—	—	—	Н
19	Валерия С.	—	+	—	+	—	+	—	+	Н
20	Алина С.	+	+	+	—	+	—	—	—	В
21	Анна С.	+	—	+	+	—	—	—	—	С
22	Дарья Т.	—	+	+	—	+	+	—	—	Н
23	Елена Ф.	+	+	+	+	—	+	—	+	В

Констатирующий этап показал, что уровень знания у детей о множестве недостаточен. Почти все дети умеют сравнивать множества, считать количество элементов множества, но названия множествам дают с ошибками.

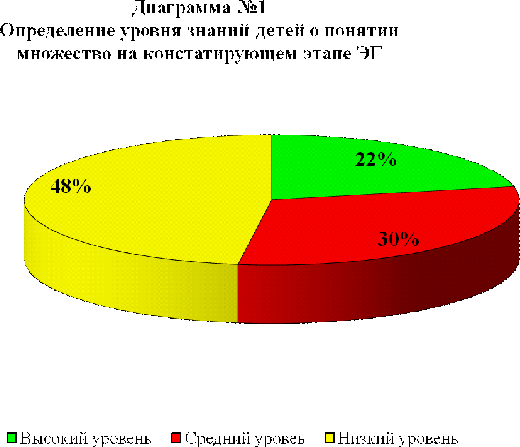
Анализируя работы детей ЭГ, которые были выполнены на констатирующем этапе, была составлена таблицы результатов и определен уровень знаний о множестве, которые представлены в таблице №3 и на диаграмме №1.

Для этого нами были разработаны критерии оценки уровня знаний:

• высокий уровень;
• средний уровень;
• низкий уровень.

Высокий уровень: характеризуется наличием знаний о множестве, умением сравнивать множества по количеству элементов, и умением давать им названия.

Средний уровень: характеризуется наличием элементарных, но не вполне систематизированных представлений о множестве, умением сравнивать множества по количеству элементов, и умением давать им названия. Интерес к множеству носит систематический характер.

Низкий уровень: характеризуется незнанием понятия «множество», неумением сравнивать множества по количеству элементов, и неумением давать им названия.

Таблица№3 Таблица определения уровня знаний у детей ЭГ на констатирующем этапе

Имя, фамилия	Знание понятия множество	Умение сравнивать множества по количеству элементов	Умение давать названия множествам	Уровень знаний
Арина Е.	+	+	+/-	В
Антон Г.	—	+/-	+/-	С
Артем С.	—	+/-	—	Н
Вера К.	+	+	+/-	В
Вероника Г.	—	—	+/-	Н
Вика С.	+/-	+	+	В
Даша М.	+	—	+/-	С
Егор К.	—	+/-	+	Н
Женя З.	—	+	—	Н
Катя А.	—	+	+/-	С
Коля С.	+	+/-	+	В
Лера Ж.	+/-	+	+	В
Лиза В.	—	+/-	+	С
Марьяна Г.	—	+/-	—	Н
Маша П.	+	—	+/-	С
Настя С.	—	+/-	—	Н
Самира Н.	+/-	+/-	+	С
Сережа К.	+/-	—	—	Н
Соня К.	+	+/-	—	С
Эмиль А.	+/-	—	—	Н
Юля У.	+/-	—	—	Н
Яна Я.	—	—	—	Н
Ярослав Б.	—	+/-	—	Н

Преобладание: в — высокий уровень

с- средний уровень н — низкий уровень

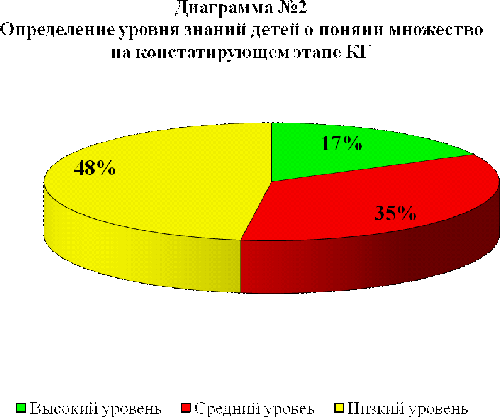
Полученные результаты по определению уровня знания детей КГ представлены в таблице №4 и на диаграмме№2

Таблица№4 Таблица определения уровня знаний у детей КГ на констатирующем этапе

Имя, фамилия	Знание понятия множество	Умение сравнивать множества по количеству элементов	Умение давать названия множествам	Имя, фамилия
Настя А.	—	+/-	+/-	С
Алевтина А.	+/-	—	+/-	С
Елена А.	—	—	—	Н
Дмитрий Б.	+/-	+	+	В
Софья Б.	+/-	+/-	+/-	С
Полина Б.	+/-	—	—	Н
Анна В.	—	+/-	+/-	С
Александр Г.	+/-	—	—	Н
Никита Г.	+/-	—	—	Н
Стефания Д.	+	—	+/-	С
Мария Е.	+/-	+	+	В
Стася И.	—	+/-	—	Н
Роман И.	—	+/-	—	Н
Мария К.	—	+/-	—	Н
Надежда К.	+	—	+/-	С
Никита К.	—	+/-	—	Н
Пётр Л.	+	+/-	+/-	С
Николай П.	—	+/-	—	Н
Валерия С.	+/-	—	—	Н
Алина С.	+/-	+	+	В
Анна С.	+/-	—	+/-	С
Дарья Т.	—	+/-	—	Н
Елена Ф.	+	+	+	В

Преобладание: в — высокий уровень

с — средний уровень н — низкий уровень

Все вышеизложенное определило нашу дальнейшую работу по формированию у детей младшего школьного возраста понятия «множество».

2.2 Разработка уроков и дидактических игр по обучению детей младшего школьного возраста понятию «множество» с использованием мультимедийных технологий

Умение выделять множества и давать им названия — это только первоначальный этап в формировании представлений о множестве.

Важное место занимает при изучении этого материала наглядность. Цель метода наглядности — обогащение и расширение непосредственного, чувственного опыта детей, развитие наглядности, изучение конкретных свойств предметов, создание условий для перехода к абстрактному мышлению, опоры для самостоятельного учения и систематизации изученного. Применяется естественная, рисуночная, объемная, звуковая и графическая наглядность.

Средство наглядности разнообразны: предметы и явления окружающей действительности, действия учителя и детей, изображения реальных предметов, процессов (рисунков, картины), модели предметов (игрушки, вырезки из картона), символические изображения (карты, таблицы, схемы).

Наглядные методы применяются на всех этапах педагогического процесса.

Постоянно должна проводиться работа, связанная с наблюдением, сравниванием групп предметов. Широко должна использоваться наглядность, дидактический материал.

Геометрический прием условного обозначения вещей и их отношения рисунком, чертежом и т.п. является средством более легкого представления и запоминания изучаемого.

При проведении формирующего эксперимента были поставлены и решены задачи:

разработка дидактических игр и презентаций, направленных на развитие представлений о множестве.

создать развивающую среду;

• определить наиболее оптимальный подход для детей младшего школьного возраста.

Мир ребенка очень красочный и эмоциональный. Приходя на урок, хочется, чтобы детям было интересно, что бы они хорошо усвоили материал. Для этого нами были разработаны уроки с использованием мультимедийных презентаций. Слайды презентаций в программе PowerPoint — это удобный и результативный способ предоставить детям знания о предметах, которые его окружают. Презентация совмещает в себе звук, красочное изображение, что значительно улучшает восприятие информации. Показ презентации можно сравнить с показом красивой детской книги, где на всех страницах большая яркая картинка с подписью. Все это помогает детям легче запомнить сложную информацию.

Одна из важнейших задач учителя в свете ФГОС — научить ученика жить в информационном мире. И здесь встаёт вопрос об ИКТ-компетентности педагога, т.е. о знании новых информационных технологий и умении ими пользоваться.

Опыт работы показал, что использование современных ИКТ- технологий на уроках:

• активизирует познавательную деятельность обучающихся;
• повышает мотивацию обучающихся к изучаемому предмету;
• экономит время на объяснение материала;
• позволяет выйти за рамки школьных учебников, дополнить и углубить их содержание;
• позволяет дифференцировать и индивидуализировать работу обучающихся;
• даёт возможность увеличить накопляемость оценок;
• создаёт комфортность на уроках.

Активизация познавательной деятельности учащихся при применении ИКТ достигается за счёт:

• дифференциации вопросов к одному и тому же заданию;
• подбора интересного материала;
• более высокого темпа работы обучающихся.

Поэтому нами использовалась работа с MacBookами, в частности, в программе «ПервоЛого». Такие уроки вызывают интерес у младших школьников.

На формирующем этапе нами были проведены уроки с использованием мультимедийных технологий, разработаны презентации для развития познавательного интереса детей, а также дидактические игры, направленные на формирование у детей младшего школьного возраста представлений о множестве.

Исследовательская работа проводилась в экспериментальной группе. На данном этапе были проведены следующие уроки с использованием мультимедийных технологий.

Урок. Тема «Множество. Число элементов множества. Подмножество» Цели урока: познакомить детей с понятиями «множество», «элемент множества», «подмножество»; научить определять число элементов множества;

• учить определять принадлежность элементов заданному множеству (множествам);
• учить определять принадлежность элементов множеству и его подмножеству (подмножествам).

1. Повторение.

Игра «Классификация»

Цель игры: развитие способности логически мыслить, находить общие характеристики (свойства) предметов.

Класс делится на 2 команды. Каждой из двух команд детей предлагаются одинаковые наборы предметов. Нужно как можно быстрее разделить эти предметы на несколько групп. После того, как задание будет выполнено, представитель каждой команды объясняет, по какому признаку была произведена классификация.

Например, совокупность предметов, предложенных детям, может быть такой: магнитофон, булка, пластинка, сыр, масло, мороженое, книга. (Предметы для отдыха, продукты).

2. Множество. Элемент множества. Число элементов множества.

Вступительное слово учителя. (слайд № 3 презентации)

— Дорогие ребята, сегодня мы с вами начинаем путешествие по замечательному острову, который имеет название Множество. На этом острове живут необычные жители — они так любят порядок, что буквально все, что их окружает, объединяют в множества. Проводниками у нас будут веселые человечки.

— Итак, вперед! Пока мы плывем к берегу, давайте с вами изучим историю названия острова. Как вы думаете, от какого слова происходит слово «множество»? (От слова «много».) В математике словом «множество» обозначают не обязательно большую группу предметов или существ.

Элементов в множестве может быть и миллион, и десяток, и один или вообще не быть (т.е. нуль элементов):

• Давайте посмотрим на примеры и определим, сколько элементов в каждом множестве:

(на доске развешаны плакаты с множествами или это могут быть слайды №№ 4 — 7 презентации):

• Множество может включать совсем немного элементов и даже быть пустым — не иметь ни одного элемента. (Так же, как среди чисел есть число 0, которое обозначает отсутствие количества, веса, длины и т.д.).

Тренировочные упражнения.

• А теперь выполните задания 1 и 2 (в рабочей тетради).