Понятие «развитие математических способностей» является довольно сложным, комплексным и многоаспектным. Оно состоит из взаимосвязанных и взаимообусловленных представлений о пространстве, форме, величине, времени, количестве, их свойствах и отношениях, которые необходимы для формирования у ребёнка «жизненных» и «научных» понятий. Под математическим развитием дошкольников понимаются качественные изменения в познавательной деятельности ребёнка, которые происходят в результате формирования элементарных математических представлений и связанных с ними логических операций. Математический развитие — значимый компонент в формировании «картины мира» ребёнка. Следовательно, одной из наиболее важных задач воспитателя и родителей — развить у ребёнка интерес к математике в дошкольном возрасте. Приобщение к этому предмету в игровой и занимательной форме поможет ребёнку в дальнейшем быстрее и легче усваивать школьную программу. А главная цель: вырастить детей людьми, умеющими думать, правильно ориентироваться во всем, что их окружает, правильно оценивать различные ситуации, принимать самостоятельные решения. Формированию у ребёнка математических представлений способствует использование разнообразных дидактических игр. В игре ребёнок приобретает новые знания, умения, навыки. Игры, способствующие развитию восприятия, внимания, памяти, мышления, развитию творческих способностей, направлены на умственное развитие дошкольника в целом. На занятиях по развитию логики и развитию элементарных математических представлений мы стараемся не только дать детям базисные знания по математике, самое главная наша задача — развивать мышление ребёнка, т. е. его умственные способности, которые необходимы, как и для успешного обучения в школе, так и нужны для будущей взрослой жизни.
Математический стиль мышления — это не всегда сложно. Математика вполне может быть лёгкой, интересной забавой для ребёнка, она может стать изящной игрой, войти в жизнь естественно, создавая предпосылки для изучения точных наук в дальнейшем. Ошибочно полагать, что для успешного постижения математики ребёнок должен как можно раньше научиться считать до ста или делить в столбик. Вовсе нет. Ребёнок лишь должен как можно раньше усвоить основные математические идеи и понятие. В игре это происходит особенно легко. В работе с детьми мы широко используем разнообразный занимательный материал, в частности цветные палочки Х. Кюизенера (бельгийского математика), рекомендованными для обучения детей с 3-х лет математике. Работа над развитием мышления ребёнка, начиная с раннего детства, будет эффективной тогда, когда педагог включит ее в любой вид деятельности, в занятия и труд, в игры и наблюдения природы, в обсуждении поступка и в рисовании с натуры или по представлению. Речь, очень рано включаясь в этот процесс, играет в нем все большую роль, изменяя всю мыслительную деятельность. Потребность в целенаправленном формировании приёмов мышления в процессе изучения конкретных образовательных дисциплин уже осознаётся психологами и педагогами. Сегодня остаётся открытым вопрос о приемлемых и действенных формах развития дошкольников, позволяющих решать проблему развития логического мышления в условиях дошкольного учреждения. Актуальность темы обусловлена тем, что Концепция по дошкольному образованию, ориентиры и требования к обновлению содержания дошкольного образования очерчивают ряд достаточно серьёзных требований к познавательному развитию дошкольников, частью которого является формирование элементарных математических представлений.
«Методическое руководство математическим развитием детей ...
... «математическое развитие дошкольников». 3. Провести анализ программ математического развития дошкольников. 4. Выявить основные формы, методы и средства методической работы по математическому развитию детей. 5. Определить состояние методической работы на современном этапе. 6. Разработать рабочую программу по математическому развитию ...
Цель исследования:
Глава I. Теоретические основы логико-математических игр в развитие логического мышления старших дошкольников. 1.1 Логико-математические игры как средство развития математических способностей детей дошкольного возраста.
Интерес к математике у старших дошкольников поддерживается занимательностью самих задач, вопросов, заданий. Говоря о занимательности, мы имеем в виду не развлечение детей пустыми забавами, а занимательность содержания математических заданий. Педагогически оправданная занимательность имеет целью привлечь внимание детей, усилить его, активизировать их мыслительную деятельность. Занимательность в этом смысле всегда несёт элементы остроумия, игрового настроя, праздничности. Занимательность служит основой для проникновения в сознание ребят чувства прекрасного в самой математике. Занимательность характеризуется наличием лёгкого и умного юмора в содержании математических заданий, в их оформлении, в неожиданной развязке при выполнении этих заданий. Юмор должен быть доступен пониманию детей. Поэтому воспитатели добиваются от самих детей доходчивого разъяснения сущности лёгких задач-шуток, весёлых положений, в которых иногда оказываются ученики во время игр, т.е. добиваются понимания сущности самого юмора и его безобидности. Чувство юмора обычно проявляется тогда, когда находят отдельные весёлые чёрточки в различных ситуациях. Чувство юмора, если им обладает человек, смягчает восприятие отдельных неудач в сложившейся обстановке.
Лёгкий юмор должен быть добрым, создавать бодрое, приподнятое настроение. Атмосфера лёгкого юмора создаётся путём включения в занятия задач-рассказов, заданий героев весёлых детских сказок, включения задач-шуток, путём создания игровых ситуаций и весёлых соревнований. Дидактическая игра как средство обучения математики. На уроках математики большое место занимают игры. Это главным образом дидактические игры, т.е. игры, содержание которых способствует либо развитию отдельных мыслительных операций, либо освоению вычислительных приёмов, навыков в беглости счета. Целенаправленное включение игры повышает интерес детей к занятиям, усиливает эффект самого обучения. Создание игровой ситуации приводит к тому, что дети, увлечённые игрой, незаметно для себя и без особого труда и напряжения приобретают определённые знания, умения и навыки. В старшем дошкольном возрасте у детей сильна потребность в игре, поэтому воспитатели детского сада включают ее в уроки математики. Игра делает уроки эмоционально насыщенными, вносит бодрый настрой в детский коллектив, помогает эстетически воспринимать ситуацию, связанную с математикой. Дидактическая игра является ценным средством воспитания умственной активности детей, она активизирует психические процессы, вызывает у учащихся живой интерес к процессу познания.
Особенности воспитания детей игрой
... об особенностях воспитания детей игрой. В настоящее время тема воспитания ребёнка весьма актуальна. В основном воспитание ребёнка происходит в семье, а также в образовательно-воспитательных ... Можно выделить следующие закономерности: Воспитание ребёнка Любая воспитательная задача решается через активные действия: физическое развитие- через физические упражнения, интеллектуальное- через мыслительную ...
В ней дети охотно преодолевают значительные трудности, тренируют свои силы, развивают способности и умения. Она помогает сделать любой учебный материал увлекательным, вызывает у детей глубокое удовлетворение, создаёт радостное рабочее настроение, облегчает процесс усвоения знаний. В дидактических играх ребёнок наблюдает, сравнивает, сопоставляет, классифицирует предметы по тем или иным признакам, производит доступные ему анализ и синтез, делает обобщения. Дидактические игры предоставляют возможность развивать у детей произвольность таких психических процессов, как внимание и память. Игровые задания развивают у детей смекалку, находчивость, сообразительность. Многие из них требуют умения построить высказывание, суждение, умозаключение; требуют не только умственных, но и волевых усилий – организованности, выдержки, умения соблюдать правила игры, подчинять свои интересы интересам коллектива. Однако не всякая игра имеет существенное образовательное и воспитательное значение, а лишь та, которая приобретает характер познавательной деятельности.
Дидактическая игра обучающего характер сближает новую, познавательную деятельность ребёнка с уже привычной для него, облегчая переход от игры к серьёзной умственной работе. Дидактические игры особенно необходимы в обучении и воспитании детей шестилетнего возраста. В них удаётся сконцентрировать внимание даже самых инертных детей. Вначале дети проявляют интерес только к игре, а затем и к тому учебному материалу, без которого игра невозможна. Чтобы сохранить саму природу игры и в то же время успешно осуществлять обучение ребят математике, необходимы игры особого рода. Они должны быть организованы так, чтобы в них: во-первых, в качестве способа выполнения игровых действий возникала объективная необходимость в практическом применении счета; во-вторых, содержание игры и практические действия были бы интересными и предоставляли возможность для проявления самостоятельности и инициативы детей. б) Логические упражнения на занятиях математики. Логические упражнения представляют собой одно из средств, с помощью которого происходит формирование у детей правильного мышления. Когда говорят о логическом мышлении, то имеют в виду мышление, по содержанию находящееся в полном соответствии с объективной реальностью Логические упражнения позволяют на доступном детям математическом материале, в опоре на жизненный опыт строить правильные суждения без предварительного теоретического освоения самих законов и правил логики.
В процесс логических упражнений дети практически учатся сравнивать математические объекты, выполнять простейшие виды анализа и синтеза, устанавливать связи между родовыми и видовыми понятиями. Чаще всего предлагаемые детям логические упражнения не требуют вычислений, а лишь заставляют детей выполнять правильные суждения и доказательства. Сами же упражнения носят занимательный характер, поэтому они содействуют возникновению интереса у детей к процессу мыслительной деятельности. А это одна из кардинальных задач учебно-воспитательного процесса старших дошкольников. Вследствие того, что логические упражнения представляют собой упражнения в мыслительной деятельности, а мышление старших дошкольников в основном конкретное, образное, то на уроках я применяю наглядность. В зависимости от особенностей упражнений в качестве наглядности применяют рисунки, чертежи, краткие условия задач, записи терминов-понятий. Народные загадки всегда служили и служат увлекательным материалом для размышления. В загадках обычно указываются определённые признаки предмета, по которым отгадывают и сам предмет. Загадки – это своеобразные логические задачи на выявление предмета по некоторым его признакам. Признаки могут быть разными.
По Педагогике «Роль пальчиковых игр и упражнения для развития ...
... творчества. Цель нашей работы: определение своеобразия «пальчиковых» игр в развитии мелкой моторики и речи детей дошкольного возраста; создать условия для развития речи дошкольников через пальчиковые игры; Задачи: выявить зависимость речи детей от развития мелкой моторики рук; изучить ...
Они характеризуют как качественную, так и количественную сторону предмета. Для уроков математики подбираются такие загадки, в которых главным образом по количественным признакам наряду с другими находится сам предмет. Выделение количественной стороны предмета (абстрагирование), а также нахождение предмета по количественным признакам – полезные и интересные логико-математические упражнения. Сюжетно-ролевые игры можно обозначить как творческие. Их основное отличие от других игр заключается в самостоятельности создания сюжета и правил игры и их выполнение. Наиболее притягательную силу для старших дошкольников имеют те роли, которые дают им возможность проявлять высокие моральные качества личности: честность, смелость, товарищество, находчивость, остроумие, смекалку. Поэтому такие игры содействуют не только выработке отдельных математических навыков, но и остроты и логичности мысли. В частности, игра содействует воспитанию дисциплинированности, т.к. любая игра проводится по соответствующим правилам.
Включаясь в игру, ребёнок выполняет определённые правила; при этом он подчиняется самим правилам не по принуждению, а совершенно добровольно, иначе не будет игры. А выполнение правил бывает связано с преодолением трудностей, с проявлением настойчивость.
Однако, несмотря на всю важность и значение игры в процессе урока, она не самоцель, а средство для развития интереса к математике. Математическая сторона содержания игры всегда должна отчётливо выдвигаться на передний план. Только тогда она будет выполнять свою роль в математическом развитии детей и воспитании интереса их к математике. В дидактике имеются разнообразные развивающие материалы. Наиболее эффективным пособием являются логические блоки, разработанные венгерским психологом и математиком Дьенешем, для развития раннего логического мышления и для подготовки детей к усвоению математики. Блоки Дьенеша представляют собой набор геометрических фигур, который состоит из 48 объёмных фигур, различающихся по форме (круги, квадраты, прямоугольники, треугольники), по цвету (жёлтые, синие, красные), размеру(большие и маленькие) по толщине(толстые и тонкие).То есть, каждая фигура характеризуется четырьмя свойствами: цветом, формой, размером, толщиной. В наборе даже нет двух фигур, одинаковых по всем свойствам. В своей практике воспитатели детских садов используют в основном плоские геометрические фигуры. Весь комплекс игр и упражнений с блоками Дьенеша – это длинная интеллектуальная лестница, а сами игры и упражнения – её ступеньки. На каждую из этих ступенек ребёнок должен встать. Логические блоки помогают ребёнку овладеть мыслительными операциями и действиями, к ним относятся: выявление свойств, их сравнение, классификация, обобщение, кодирование и декодирование, а так же логические операции. Кроме того, блоки могут закладывать в сознание детей начало алгоритмической культуры мышления, развивать у детей способность действовать в уме, осваивать представления о числах и геометрических фигурах, пространственную ориентацию.
Игры, как манипуляции с игрушками и предметами. Игрушки и предметы ...
... детей дошкольного возраста будет более эффективным, если вы работаете с ними, опираться на вид деятельности, и построить свою работу в игровой форме, ... развитие речи, воображения и творчества у детей дошкольного возраста. Играть догадался, что нарисовано на картинке, ребенок прибегает к имитации движений (например, животного, птицы). В этих играх, является качество личности ребенка, как способность ...
В процессе разнообразных действий с блоками дети сначала осваивают умение выявлять и абстрагировать в предметах одно свойство (цвет, форму, размер, толщину), сравнивать, классифицировать и обобщать предметы по одному из этих свойств. Затем они овладевают умениями анализировать, сравнивать, классифицировать и обобщать предметы сразу по двум свойствам (цвету и форме, форме и размеру, размеру и толщине ит.д.), несколько позже по трём (цвету, форме, размеру; форме, размеру, толщине и т.д.) и по четырём свойствам(цвету, форме, размеру, толщине), при этом развивая логическое мышление детей. В одном и том же упражнении можно варьировать правилами выполнения задания с учётом возможностей детей. Например, несколько детей строят дорожки. Но одному ребёнку предлагается построить дорожку так, чтобы рядом не было блоков одинаковой формы (оперирование одним свойством), другому — чтобы рядом не было одинаковых по форме и по цвету (оперирование сразу двумя свойствами).
В зависимости от уровня развития детей можно использовать не весь комплекс, а какую-то его часть, сначала блоки разные по форме и по цвету, но одинаковые по размеру и толщине, затем разные по форме, цвету и размеру, но одинаковые по толщине и в конце полный комплекс фигур. Это очень важно: чем разнообразней материал, тем сложнее абстрагировать одни свойства от других, а значит, и сравнивать, и классифицировать, и обобщать. С логическими блоками ребёнок выполняет различные действия: выкладывает, меняет местами, убирает, прячет, ищет, делит, а по ходу действия рассуждает. Итак, играя с блоками, ребёнок приближается к пониманию сложных логических отношений между множествами. От игры с абстрактными блоками дети легко переходят к играм с реальными множествами, с конкретным материалом. математика. Овладение детьми математикой происходит в процессе специальных занятий, основной целью которых и является формирование у детей предпосылок к обучению письму счету. Ведущей задачей при формировании математических понятий является: наблюдение (изменение, моделирование, построение) объектов с целью выявления их свойств; сравнение объектов и их свойств: анализ свойств, в ходе которого надо определить, какие из них являются общими, отличительными, существенными, а какие несущественными; установление и использование аналогий; обобщение, формулировка суждений об общих существенных признаках объектов; классификаций — разбивка множества изучаемых понятий на классы и виды и т.
п. т. е. на задания, которые формируют умственную деятельность ребенка и развивают мыслительные операции. Развитие умения ориентироваться в некоторых скрытых существенных математических связях, отношениях, зависимостях (поровну, больше, меньше, целое, часть, зависимость между величинами и др.); Обучение овладением способами установления разного рода математических связей, отношений; понятия, что самыми очными способами установления количественных отношений является счет предметов и измерение величин . Особенность преемственности дошкольного и начального образования в том, что воспитатель должен учитывать двусторонность данного процесса. С одной стороны, признавать само ценность дошкольного детства с опорой на ведущую — игровую — деятельность, с другой создавать условия для элементов учебной деятельности. В детском саду уделяется внимание развитию специальной терминологии: названиям чисел, действий (прибавления и отнимания), знаков (плюс, минус, равно).
Психологическая коррекция особенностей развития детей при сложных ...
... данной темы определяется необходимостью развития системы специального образования детей с ДЦП, имеющими задержку психического развития в связи с гуманистическими тенденциями развития общества и степенью востребованности ... имеет первичная потенциальная сохранность интеллектуальной сферы. Оптимальное развитие такого ребенка может происходить только при условии адекватного воспитания и обучения. В ...
В школе углубляется процесс обогащения речи детей специальными терминами. Дети усваивают названия данных и искомых, компонентов действий сложения и вычитания, учатся читать и записывать самые простые выражения и т.д.
1.2Сущность и особенности развития математических способностей детей дошкольного возраста.
В связи с проблемой формирования и развития способностей следует указать, что целый ряд исследований психологов направлен на выявление структуры способностей дошкольников к различным видам деятельности. При этом под способностями понимается комплекс индивидуально – психологических особенностей человека, отвечающих требованиям данной деятельности и являющиеся условием успешного выполнения. Таким образом, способности – сложное, интегральное, психическое образование, своеобразный синтез свойств, или, как их называют компонентов. Общий закон образования способностей состоит в том, что они формируются в процессе овладения и выполнения тех видов деятельности, для которых они необходимы. Способности не есть нечто раз и навсегда предопределённое, они формируются и развиваются в процессе обучения, в процессе упражнения, овладения соответствующей деятельностью, поэтому нужно формировать, развивать, воспитывать, совершенствовать способности детей и нельзя заранее точно предвидеть как далеко может пойти это развитие. Говоря о математических способностях как особенностях умственной деятельности, следует прежде всего указать на несколько распространённых заблуждений. Во-первых, многие считают, что математические способности заключаются прежде всего в способности к быстрому и точному вычислению (в частности в уме).
На самом деле вычислительные способности далеко не всегда связаны с формированием подлинно математических (творческих) способностей. Во-вторых, многие думают, что способные к математике школьники отличаются хорошей памятью на формулы, цифры, числа. Однако, как указывает академик А. Н. Колмогоров, успех в математике меньше всего основан на способности быстро и прочно запоминать большое количество фактов, цифр, формул. Наконец, считают, что одним из показателей математических способностей является быстрота мыслительных процессов. Особенно быстрый темп работы сам по себе не имеет отношения к математических способностям. Ребёнок может работать медленно и неторопливо, но в то же время вдумчиво, творчески, успешно продвигаясь в усвоении математики. Крутецкий В.А в книге «Психология математических способностей дошкольников» различает девять способностей математических способностей: 1)Способность к формализации математического материала, к отделению формы от содержания, абстрагированию от конкретных количественных отношений и пространственных форм и оперированию формальными структурами. 2) Способность обобщать математический материал, вычленять главное, отвлекаясь от несущественного, видеть общее во внешне различном; 3) Способность к оперированию числовой и знаковой символикой; 4) Способность к «последовательному, правильно расчленённому логическому рассуждению», связанному с потребностью в доказательствах, обосновании,выводах; 5) Способность сокращать процесс рассуждения, мыслить свёрнутыми структурами; 6) Способность к обратимости мыслительного процесса.
Воспитание и обучение детей с отклонениями в развитии
... отмечаются отклонения в развитии звуковой стороны речи. Иногда неправильное звукопроизношение связано с дефектной речью окружающих, ребенок говорит плохо, подражая неправильной речи взрослых. Нарушение звукопроизно-шения может быть следствием педагогической запущенности, ...
7) Гибкость мышления, способность к переключению от одной умственной операции к другой, свобода от сковывающего влияния шаблонов и трафаретов; 8) Математическая память. Можно предположить, что её характерные особенности также вытекают из особенностей математической науки, что это память на обобщения, формализованные структуры, логические схемы; 9) Способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики как геометрия.
Многие родители полагают, что главное при подготовке к школе — это познакомить ребёнка с цифрами и научить его писать, считать, складывать и вычитать (на деле это обычно выливается в попытку выучить наизусть результаты сложения и вычитания в пределах 10) Однако при обучении математике по учебникам современных развивающих систем (система Л. В. Занкова, система В. В. Давыдова, система «Гармония», «Школа 2100» и др.) эти умения очень недолго выручают ребёнка на уроках математики. Запас заученных знаний кончается очень быстро (через месяц-два), и несформированность собственного умения продуктивно мыслить (то есть самостоятельно выполнять указанные выше мыслительные действия. В то же время ребёнок с развитым логическим мышлением всегда имеет больше шансов быть успешным в математике, даже если он не был заранее научен элементам школьной программы (счету, вычислениям и т. п.).
Не случайно в последние годы во многих школах, работающих по развивающим программам, проводится собеседование с детьми, поступающими в первый класс, основным содержанием которого являются вопросы и задания логического, а не только арифметического, характера. 2)Закономерен ли такой подход к отбору детей для обучения? Да, закономерен, поскольку учебники математики этих систем построены таким образом, что уже на первых уроках ребёнок должен использовать умения сравнивать, классифицировать, анализировать и обобщать результаты своей деятельности. Однако не следует думать, что развитое логическое мышление — это природный дар, с наличием или отсутствием которого следует смириться.Существует большое количество исследований, подтверждающих, что развитием логического мышления можно и нужно заниматься (даже в тех случаях, когда природные задатки ребёнка в этой области весьма скромны).
Прежде всего разберёмся в том, из чего складывается логическое мышление. Логические приёмы умственных действий — сравнение, обобщение, анализ, синтез, классификация, сериация, аналогия, систематизация, абстрагирование — в литературе также называют логическими приёмами мышления. При организации специальной развивающей работы над формированием и развитием логических приёмов мышления наблюдается значительное повышение результативности этого процесса независимо от исходного уровня развития ребёнка. Для выработки определённых математических умений и навыков необходимо развивать логическое мышление дошкольников. В школе им понадобятся умения сравнивать, анализировать, конкретизировать, обобщать. Поэтому необходимо научить ребёнка решать проблемные ситуации, делать определённые выводы, приходить к логическому заключению. Решение логических задач развивает способность выделять существенное, самостоятельно подходить к обобщениям. Логические игры математического содержания воспитывают у детей познавательный интерес, способность к творческому поиску, желание и умение учиться. Необычная игровая ситуация с элементами проблемности, характерными для каждой занимательной задачи, всегда вызывает интерес у детей.
Эстетическое, физическое, нравственное воспитание детей со сложными ...
... педагогике сенсорное воспитание рассматривается как основа умственного, эстетического, физического, трудового воспитания ребенка. С учетом своеобразия развития детей со сложными нарушениями развития - эстетическое воспитание обучения направлено на решение следующих задач: 1. воспитывать ...
Занимательные задачи способствуют развитию у ребёнка умения быстро воспринимать познавательные задачи и находить для них верные решения. Дети начинают понимать, что для правильного решения логической задачи необходимо сосредоточиться, они начинают осознавать, что такая занимательная задачка содержит в себе некий «подвох» и для ее решения необходимо понять, в чем тут хитрость. Логические задачки могут быть следующими. У двух сестёр по одному брату. Сколько детей в семье? (Ответ : 3) . Очевидно, что конструктивная деятельность ребёнка в процессе выполнения данных упражнений развивает не только математические способности и логическое мышление ребёнка, но и его внимание, воображение, тренирует моторику, глазомер, пространственные представления, точность и т. д. Каждое из приведённых в упражнений направлено на формирование логических мыслительных приёмов.
Упражнение 1 учит анализу и сравнению; упражнение 2 учит синтезу; упражнение 3 учить, ребёнка — сравнивать: упражнение 4 сравнивать и обобщать, а также анализировать; упражнение 5 фактическая классификация по признаку. Логическое развитие ребёнка предполагает также формирование умения понимать и прослеживать причинно-следственные связи явлений и умения выстраивать простейшие умозаключения на основе причинно-следственной связи.
Таким образом, за два года до школы можно оказать значимое влияние на развитие математических способностей дошкольника. Даже если ребёнок не станет непременным победителем математических олимпиад, проблем с математикой у него в начальной школе не будет, а если их не будет в начальной школе, то есть все основания рассчитывать на их отсутствие и в дальнейшем.
Для ребят дошкольного возраста игра имеет исключительное значение: игра для них – учёба, игра для них – труд, игра для них — серьёзная форма воспитания. Игра для дошкольников – способ познания окружающего мира. Игра будет являться средством воспитания, если она будет включаться в целостный педагогический процесс. Руководя игрой, организуя жизнь детей в игре, воспитатель воздействует на все стороны развития личности ребёнка: на чувства, на сознание, на волю и на поведение в целом. Мышление человека осуществляется тремя способами, имеет три вида: наглядно-действенное, наглядно — образное, словесно-логическое. Последний вид мышления характеризуется как более высокий уровень. Для его развития можно использовать логические задачи и игры, которые тренируют не только логическое мышление, но и служит надёжной основой умственного развития, формированием интереса к математической деятельности.
Развитие мышления в старшем дошкольном возрасте
... была выбрана следующая тема курсовой работы: «Особенности развитие мышления у детей старшего дошкольного возраста». Объект исследования:, Предмет исследования: Цель: изучить психологические особенности развития мышления у старших дошкольников. Задачи: 1. Изучить литературу по теме исследования. 2. В ...
Интерес к математике является одним из условий развития математических способностей. Логические игры математического содержания воспитывают у детей познавательный интерес, способность к творческому поиску, желание и умение учиться. Необычная игровая ситуация с элементами проблемности, характерными для каждой занимательной задачи, всегда вызывает интерес у детей. Использование логических игр, направленных на решение логических задач, организованных по форме выбора одного ответа (правильного) из нескольких, развивает также и такое важное качество, как критичность, обоснованность мышления, поскольку любой выбор всегда содержит требование к его обоснованию, к объяснению того, почему выбран один, а не другой ответ. Происходит становление у детей развитых форм самосознания и самоконтроля, у них исчезает боязнь ошибочных шагов, снижается тревожность и необоснованное беспокойство. Самостоятельное решение детьми поисковых задач является условием для развития у детей характерологических черт личности, как самостоятельности в действиях, способности управлять собой в сложных ситуациях. В коллективном обсуждении решения задачи формируется такое важное качество деятельности и поведения, как осознание собственных действий, самоконтроль, возможность дать отчёт в выполняемых шагах при решении задач. Следовательно, логические задачи создают благоприятные условия для воспитания у детей культуры мышления, которая характеризуется возможностью самостоятельно управлять мыслительной деятельностью, проявлять инициативу в постановке ее целей и находить способы их достижения.
Глава II. Опытно-экспериментальная работа по исследованию уровня развития математических способностей старших дошкольников. 2.1 Обследование уровня способностей развития детей старшего дошкольного возраста.
Для выявления математических способностей детей старшего дошкольного возраста нами был проведен констатирующий эксперимент. В эксперименте принимали участие воспитанники дошкольного организаций детский сад № 6 г. Костаная группы « Жулдуз».Всего исследованием было охвачено 25 детей в возрасте 5лет 4 месяца — 5 лет 10месяцев. Использовали задание . «Упорядочивание». Цель задания. Выявить представление детей о счете предметов и об их упорядоченности.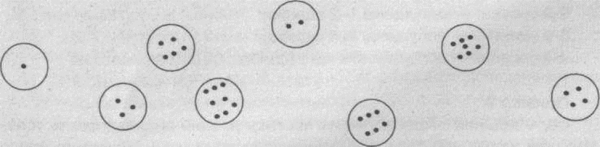 
Материалы. Картонные круги диаметром 5 см с точками. Круги располагают перед ребенком в беспорядке. Задание. В одних кругах точек мало, в других — много. Сейчас круги расположены в беспорядке. Подумай и расположи эти круги в ряд по порядку. Когда будешь искать тот или иной порядок, не забывай, что на кругах есть точки. Способ выполнения. Не следует подсказывать ребенку принцип упорядочивания. Выполнение задания самостоятельно покажет уровень с формированности его представления об упорядоченности.
Оценка задания: 1-й уровень — задание выполнено полностью верно; 2-й уровень — допущены 1-2 ошибки; 3-й уровень—допущены 3-4 ошибки; 4-й уровень — допущено более 5 ошибок. Пример 2. «Первоначальные математические представления»
Цель задания. Определить представление детей о соотношениях: больше на, меньше на; о количественном и порядковом счете, о форме простейших геометрических фигур. Материалы. Семь любых предметов или их изображений на фланелеграфе, предметы могут быть как одинаковые, так и разные. Способ выполнения. Для выполнения задания ребенку дают лист бумаги и карандаш. Задание состоит из нескольких частей. Они предлагаются последовательно. Задания. А. Нарисуй на листе столько же кругов,сколько на доске предметов Б.Нарисуй квадратов на один больше,чем кругов В.Нарисуй треугольников на два меньше,чем кругов Г.Обведи линией шесть квадратов Д.Закрась пятый круг Оценка задания (оценивается качество выполнения всех заданий в совокупности): 1-й уровень—задание выполнено полностью верно;
2-й уровень—допущены 1 -2 ошибки; 3-й уровень—допущены 3-4 ошибки;
4-й уровень — допущено более 5 ошибок.
Пример 3 Цель задания. Провести диагностику умений анализировать условия предъявленной задачи, в данном случае практического характера (планировать ход ее решения, выбирать адекватные действия, критически оценивать полученный результат).
Задание также определяет визуальную адекватность определения формы фигуры, пространственную подвижность мышления — умение мысленно перемещать и компоновать детали, адекватность визуальной оценки размеров фигур. Материалы. Белый лист бумаги с изображением контура лодочки с парусом и цветные геометрические фигуры: 4 квадрата 2×2 см, 4 прямоугольных равнобедренных треугольника с катетом 2 см, все одного цвета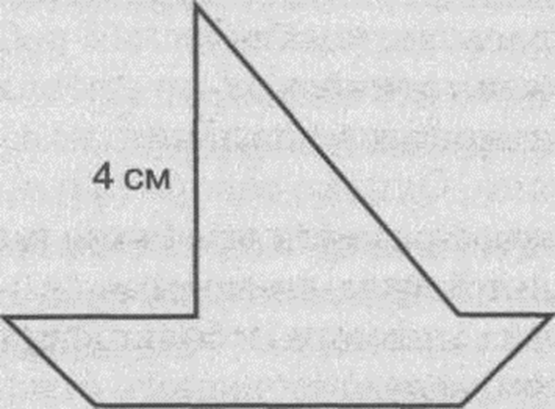 
2 см 6см Задание. Часть 1. «Раскрась» лодочку, но не карандашами, а данными фигурами. Фигуры надо уместить внутри лодочки так, чтобы они не выходили за пределы изображения. Часть 2. Оцени качество выполнения задания — все ли сделано правильно? Если ребенок сам не замечает допущенных ошибок (фигуры не прилегают друг к другу, выходят за очертания контура), педагог спрашивает, хочет ли ребенок сделать новую лодочку лучше этой.
В случае отрицательного ответа педагог не настаивает на этом. Оценка задания. А. Оценивается способ выполнения задания: обдумывал ли ребенок сначала его выполнение, планировал или работал без всякой системы, методом про и ошибок. Б.Оценивается критичность в оценке выполнения задания. В.Оценивается желание, готовность исправить допущенные ошибки. Г.Оценивается рациональность размещения фигур. Д. Оценивается темп деятельности. 1-й уровень — фигуры выложены правильно и быстро (ребенок мгновенно проанализировал задание и начал его выполнение); 2-й уровень — контур заполнен правильно, но ребенок работал методом проб и ошибок, поэтому затратил больше времени; в процессе себя корректиров 3-й уровень — только часть контура заполнена правильно, некоторые фигуры выходят за его очертания; при оценке работы ребенок ошибок не замечает, но когда педагог обращает на них его внимание, готов их исправить; 4-й уровень — контур заполнен хаотично, большинство геометрических фигур выходят за его очертания, ошибки не замечаются, желания сделать лучше при указании на них нет. Пример 4. «Заселение дома» Цель задания. Выявить способность детей к рассмотрению ситуации с разных сторон, умение переключиться с одного найденного решения на поиск другого.
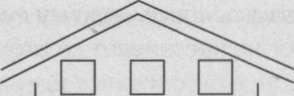
Материалы. На доске или на большом листе бумаги заранее нарисован дом,карточки с крупными изображениями «жильцов» дома; каждому ребенку дается листок с изображением такого же дома и фломастер. Задание Часть 1 (обучающая).
В доме шесть этажей. На каждом этаже — три комнаты. В каждой комнате живет один жилец: педагог показывает изображения — точка, палочка и галочка. На всех этажах они живут в разном порядке. На самом верхнем этаже в первой комнате слева — точка (рисует в окошке точку), в средней комнате — палочка (рисует палочку).Подскажите мне, кто живет в последней комнате? (Дети называют галочку, и педагог ее рисует.) Теперь нарисуйте у себя на листочке, кто, где живет на шестом этаже. (Дети рисуют, педагог проверяет правильность выполнения рисунка.) Теперь будем заселять жильцами пятый этаж: в первой комнате тоже живет точка. Подумайте, как нужно поселить палочку и галочку, чтобы они жили не в том порядке, что на шестом этаже. Размещение «жильцов» рисуется в окнах большого дома, а затем дети рисуют их у себя. На этом обучающая часть задания заканчивается. Часть 2 (основная).
— Осталось еще четыре этажа. Заселите их сами так, чтобы на каждом этаже жила одна точка, одна палочка и одна галочка, но в разном порядке. Дети выполняют задание самостоятельно. Оценка задания. 1-й уровень — задание выполнено правильно: найдены все 4 варианта размещения, не повторяющих «заселение» пятого и шестого этажей; 2-й уровень — найдено 2-3 различных варианта размещения из четырех возможных; 3-й уровень — найден один вариант размещения из четырех возможных; 4-й уровень — самостоятельных решений не найдено: повторены решения обучающего этапа или работа не выполнена (этажи остались незаселенными Пример 5. Раскрашивание фигур Цель задания. Выявить умение классифицировать наглядный материал по самостоятельно найденному основанию. Определить степень адекватности визуального восприятия формы и умение мысленно перемещать и совмещать фигуры для определения их равенства. Материалы. Каждый ребенок получает рисунок с рядом фигур, фломастеры или карандаши. Задание. Одинаковые фигуры надо закрасить одним цветом. Цвет выбирается самостоятельно. Сколько групп одинаковых фигур ребенок найдет, столько цветов использует Оценка задания. 1-й уровень — классификация выполнена правильно; выделены три группы разных фигур (3 равнобедренных треугольника, 4 равносторонних и 3 прямоугольный. 2-й уровень — одна ошибка (не различение одинаковых фигур в прямом и повернутом положении; или не различение одинаковых фигур в прямом и зеркальном положении);
3-й уровень — две ошибки (не различение одинаковых фигур в прямом и повернутом положении и не различение фигур в прямом и зеркальном положений); 4-й уровень — три ошибки (не различение одинаковых фигур в прямом и повернутом положении, в прямом и зеркальном положении, а также не различение разных фигур); бессмысленное, хаотическое раскрашивание фигур. Результаты экспресс-диагностики познавательного развития дошкольников и уровня с формированности математических представлений детей старшего дошкольного возраста старшей группы детского сада. Определим уровень познавательного развития и с формированность математически представлений дошкольников. Высокий:5-7баллов Средний:8-11баллов Низкий:12 и меньше баллов. Среди тестируемых 12 детей обнаружили высокий уровень, 9 детей средний уровень и 4 ребёнка низкий уровень познавательного развития и с формированности математических представлений. (см в приложений) Рекомендации: задания первых трёх примеров тестируют уровень развития математических представлений пространственного и конструктивного мышления, а двух последних выявляют уровень развития математического стиля мышления. Результаты констатирующего эксперимента отражены в таблице № 1 (Приложение №1) Следовательно, дети с выявленным низким уровнем познавательного развития и с формированности математических представлений нуждаются в коррекции с использованием заданий развивающих пространственное и конструктивное мышление, а так же направленные на формирование математического стиля мышления. После проведения комплекса коррекционных занятий необходима повторная диагностика.
2.2 Развитие математических способностей детей старшего дошкольного возраста средствами логико-математических игр.
Развитие математических способностей» является довольно сложным, комплексным и многоаспектным. Оно состоит из взаимосвязанных и взаимообусловленных представлений о пространстве, форме, величине, времени, количестве, их свойствах и отношениях, которые необходимы для формирования у ребенка «житейских» и «научных» понятий. В то же время специальные исследования в области развития математических способностей ребенка дошкольного и младшего школьного возраста практически отсутствуют. При этом понятие «математическое развитие» рассмотрено только в последних двух исследованиях, где оно понимается как формирование математических знаний и умений у ребенка. Таким образом, даже в рамках исследований о развитии познавательных способностей и творческой одаренности детей младшего возраста, математическому развитию ребенка уделено мало внимания. При этом понятие «математическое развитие» трактуется в основном как формирование и накопление математических знаний и умений математическим развитием дошкольников понимаются качественные изменения в познавательной деятельности ребенка, которые происходят в результате формирования элементарных математических представлений и связанных с ними логических операций. Математическое развитие значимый компонент в формировании «картины мира» ребенка. Формированию у ребенка математических представлений способствует использование разнообразных дидактических игр. В игре ребенок приобретает новые знания, умения, навыки. Игры, способствующие развитию восприятия, внимания, памяти, мышления, развитию творческих способностей, направлены на умственное развитие дошкольника в целом. «математическое развитие дошкольника – это процесс качественного изменения в интеллектуальной сфере личности, который происходит в результате формирования у ребенка математических представлений и понятий» Если бы данный подход к математическому развитию ребенка был верным, то достаточно было бы отобрать круг знаний, сообщаемых ребенку, и подобрать «под них» соответствующий метод обучения, чтобы сделать этот процесс реально продуктивным, т.е. получать в результате «поголовное» высокое математическое развитие у всех детей.
В исследовании доказано, что главным направлением организации математического развития ребенка дошкольного возраста является целенаправленное развитие конструктивного мышления, а ребенка младшего школьного возраста развитие пространственного мышления. Обучения детей математическому содержанию метода моделирования, с преимущественным использованием на каждом возрастном этапе того вида моделирования, который более всего соответствует возрастным особенностям развития мышления и других познавательных процессов. В возрасте 3-5 лет – это конструирование (вещественное моделирование), в возрасте 6-10 лет – это сочетание конструирования с графическим моделированием с постепенным перенесением акцента на второе, в возрасте 10-12 лет – это графическое моделирование с элементами конструирования там, где необходимо практическое приложение знаний и умений ребенка в математике, и с элементами логико-символического моделирования (знакового и символьного) в качестве подготовки к переходу ребенка на ведущий словесно-логический (абстрактный) тип мышления в старшем возрасте. Развития способностей следует указать, что целый ряд исследований психологов направлен на выявление структуры способностей дошкольников к различным видам деятельности. При этом под способностями понимается комплекс индивидуально – психологических особенностей человека, отвечающих требованиям данной деятельности и являющиеся условием успешного выполнения. Говоря о математических способностях как особенностях умственной деятельности, следует, прежде всего, указать на несколько распространенных среди педагогов заблуждений. Во-первых, многие считают, что математические способности заключаются, прежде всего, в способности к быстрому и точному вычислению. На самом деле вычислительные способности далеко не всегда связаны с формированием подлинно математических (творческих) способностей. Во-вторых, многие думают, что способные к математике дошкольники отличаются хорошей памятью на формулы, цифры, числа 1)Способность к формализации математического материала, к отделению формы от содержания, абстрагированию от конкретных количественных отношений и пространственных форм и оперированию формальными структурами, структурами отношений и связей: 2)Способность обобщать математический материал, вычленять главное, отвлекаясь от несущественного, видеть общее во внешне различном; 3)Способность к оперированию числовой и знаковой символикой; 4)Способность к «последовательному, правильно расчленённому логическому рассуждению», связанному с потребностью в доказательствах, обосновании, выводах; 5)Способность сокращать процесс рассуждения, мыслить свернутыми структурами; 6)Способность к обратимости мыслительного процесса (к переходу с прямого на обратный ход мысли); 7) Гибкость мышления, способность к переключению от одной умственной операции к другой, свобода от сковывающего влияния шаблонов и трафаретов; 8) Математическая память. Можно предположить, что её характерные особенности также вытекают из особенностей математической науки, что это память на обобщения, формализованные структуры, логические схемы; 9) Способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики как геометрия. Многие родители полагают, что главное при подготовке к школе – это познакомить ребенка с цифрами и научить его писать, считать, складывать и вычитать (на деле это обычно выливается в попытку выучить наизусть результаты сложения и вычитания в пределах 10)Однако при обучении математике по учебникам современных развивающих систем (система Л. В. Занкова, система В. В. Давыдова, система «Гармония», «Школа 2100» и др.) эти умения очень недолго выручают ребенка на уроках математики. Запас заученных знаний кончается очень быстро (через месяц-два), и несформированность собственного умения продуктивно мыслить (то есть самостоятельно выполнять указанные выше мыслительные действия на математическом содержании) очень быстро приводит к появлению «проблем с математикой». В то же время ребенок с развитым логическим мышлением всегда имеет больше шансов быть успешным в математике, даже если он не был заранее научен элементам школьной программы (счету, вычислениям и т. п.).
Не случайно в последние годы во многих школах, работающих по развивающим программам, проводится собеседование с детьми, поступающими в первый класс, основным содержанием которого являются вопросы и задания логического, а не только арифметического, характера. Закономерен ли такой подход к отбору детей для обучения? Да, закономерен, поскольку учебники математики этих систем построены таким образом, что уже на первых уроках ребенок должен использовать умения сравнивать, классифицировать, анализировать и обобщать результаты своей деятельности.
Однако не следует думать, что развитое логическое мышление – это природный дар, с наличием или отсутствием которого следует смириться. Существует большое количество исследований, подтверждающих, что развитием логического мышления можно и нужно заниматься (даже в тех случаях, когда природные задатки ребенка в этой области весьма скромны).
Прежде всего разберемся в том, из чего складывается логическое мышление. Логические приемы умственных действий – сравнение, обобщение, анализ, синтез, классификация, сериация, аналогия, систематизация, абстрагирование – в литературе также называют логическими приемами мышления. При организации специальной развивающей работы над формированием и развитием логических приемов мышления наблюдается значительное повышение результативности этого процесса независимо от исходного уровня развития ребенка. Логические игры математического содержания воспитывают у детей познавательный интерес, способность к творческому поиску, желание и умение учиться. Необычная игровая ситуация с элементами проблемности, характерными для каждой занимательной задачи, всегда вызывает интерес у детей. Занимательные задачи способствуют развитию у ребенка умения быстро воспринимать познавательные задачи и находить для них верные решения. Дети начинают понимать, что для правильного решения логической задачи необходимо сосредоточиться, они начинают осознавать, что такая занимательная задачка содержит в себе некий «подвох» и для ее решения необходимо понять, в чем тут хитрость.
Заключения
Математическое развитие детей старшего дошкольного возраста в конкретном образовательном учреждении (детский сад, группы развития, группы дополнительного образования, прогимназия и т. д.) проектируется на основе концепции дошкольного учреждения, целей и задач развития детей, данных диагностики, прогнозируемых результатов. Концепцией определяется соотношение пред математического и пред логического компонентов в содержании образования. От этого соотношения зависят прогнозируемые результаты: развитие интеллектуальных способностей детей старшего дошкольного возраста, их логического, творческого или критического мышления; формирование представлений о числах, вычислительных или комбинаторных навыках, способах преобразования объектов и т. д. Ориентировка в современных программах развития и воспитания детей в детском саду, изучение их дает основание для выбора методики. В современные программы («Развитие», «Радуга», «Детство», «Истоки» и др.), как правило, включается то логико-математическое содержание, освоение которого способствует развитию познавательно-творческих и интеллектуальных способностей детей. Эти программы реализуются через деятельностные личностно-ориентированные развивающие технологии и исключают «дискретное» обучение, т. е. раздельное формирование знаний и умений с последующим закреплением. Формирование у детей старшего дошкольного возраста общих понятий имеет важное значение для дальнейшего развития мышления в школьном возрасте.У детей дошкольного возраста происходит интенсивное развитие мышления. Ребёнок приобретает ряд новых знаний об окружающей действительности и вместе с тем научается анализировать, синтезировать, сравнивать, обобщать свои наблюдения, т. е. производить простейшие умственные операции. Важнейшую роль в умственном развитии ребёнка играет воспитание и обучение. Воспитатель знакомит ребёнка с окружающей действитель ностью, сообщает ему ряд элементарных знаний об явлениях природы и общественной жизни, без чего развитие мышления было бы невозможно. Однако следует указать, что простое запоминание отдельных фактов, пассивное усвоение сообщаемых знаний ещё не могут обеспечить правильное развитие детского мышления. Для того чтобы ребёнок начал мыслить, перед ним необходимо поставить новую задачу, в процессе решения которой он мог бы использовать приобретённые ранее знания применительно к новым обстоятельствам. Большое значение в умственном воспитании ребёнка приобретает поэтому организация игр и занятий, которые развивали бы у ребёнка умственные интересы, ставили бы перед ним определённые познавательные задачи, заставляли бы самостоятельно производить определённые умственные операции для достижения нужного результата. Этому служат вопросы, задаваемые воспитателем во время занятий, прогулок и экскурсий, дидактические игры, носящие познавательный характер, всякого рода загадки и головоломки, специально предназначенные для стимуляции умственной активности ребёнка. Логические приемы как средство формирования логического мышления дошкольников – это сравнение, синтез, анализ, классификация, доказательство и другие – применяются во всех видах деятельности. Их используют начиная с первого класса для решения задач, выработки правильных умозаключений. Сейчас, в условиях коренного изменения характера человеческого труда, ценность такого знания возрастает. Свидетельство тому – растущее значение компьютерной грамотности, одной из теоретических основ которой является логика. Знание логики способствует культурному и интеллектуальному развитию личности. Отбирая методы и приёмы, воспитатель должен помнить, что в основе образовательного процесса лежит проблемно-игровая технология. Поэтому преимущество отдаётся игре, как основному методу обучения дошкольников, математическим развлечениям, дидактическим, развивающим, логико-математическим играм; игровым упражнениям; экспериментированию; решению творческих и проблемных задач, а также практической деятельности.
Приложение № 1
3
3
4
4
2
16
Список литературы
[Электронный ресурс]//URL: https://psychoexpert.ru/kursovaya/razvitie-matematicheskih-sposobnostey-doshkolnikov/
1.Беженова М. Математическая азбука. Формирование элементарных математических представлений. – М.: Эксмо, СКИФ,2005.
2.Белошистая А.В. Готовимся к математике. Методические рекомендации для организации занятий с детьми 5-6 лет. – М.: Ювента,2006.
3.Волчкова В.Н., Степанова Н.В. Конспекты занятий в старшей группе детского сада. Математика. Практическое пособие для воспитателей и методистов ДОУ. – М.: ТЦ «Учитель», 2007.
4.Денисова Д., Дорожин Ю. Математика для дошкольников. Старшая группа 5+. –М.:Мозаика — Синтез,2007.
5.Занимательная математика. Материалы для занятий и уроков с дошкольниками и младшими школьниками. – М.: Учитель, 2007.
6.Звонкин А.К. Малыши и математика. Домашний кружок для дошкольников.–М.:МЦНМО,МИОО,2006.
7. Кузнецова В.Г. Математика для дошкольников. Популярная методика игровых уроков. – СПб.: Оникс, Оникс-СПб, 2006.
8. Носова Е.А., Непомнящая Р.Л. Логика и математика для дошкольников.–М.:Детство-Пресс,2007.
9. Петерсон Л.Г., Кочемасова Е.Е. Игралочка. Практический курс математики для дошкольников. Методические рекомендации.–М.:Ювента,2006.
10.Сычева Г.Е. Формирование элементарных математических представлений у дошкольников. – М.: Книголюб,2007.
11.Шалаева Г. Математика для маленьких гениев дома и в детском саду. – М.: АСТ, Слово, 2009.
