«Интерактивные технологии обучения»

метки: Интерактивный, Технология, Педагогический, Задание, Метод, Знание, Величина, Логик

Актуальность темы. Современный этап развития общества характеризуется глубокими социально-экономическими преобразованиями. В связи с этим перед образованием встают новые задачи: необходимость школы ориентироваться на создание оптимальных условий для развития каждого ребенка, опираться не на заучивание, а на формирование способностей самостоятельно осмысливать окружающую действительность. В образовательных документах акцент делается на развитии инновационных образовательных технологий в учебном процессе с целью обеспечения перехода образования на новую, личностно ориентированную парадигму. Определяющей чертой личностно ориентированного обучения есть взаимопонимание, взаимодействие, творческое сотрудничество учителя и учеников.

ФГОС начального общего образования определена основная цель начального образования, которая, среди прочего, заключается во всестороннем развитии и воспитании личности через формирование у учащихся полноценных языковых умений и навыков, приобретение личного опыта культуры общения и сотрудничества в различных видах учебной деятельности, самовыражения в творческих видах задач, общеучебных и целевых компетенций. Основные направления оптимального решения таких задач непосредственно связанные с внедрением в учебный процесс интерактивных методов.

1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЯ ИНТЕРАКТИВНЫХ ТЕХНОЛОГИЙ ОБУЧЕНИЯ

1.1 Понятие «интерактивные методы»

Понятие «активные методы» появилось в отечественной и зарубежной педагогике в 20-30-х годах ХХ века. На территории России значительный вклад в разработку этих вопросов сделал Александр Григорьевич Ривин, который начал так называемый метод обучения в парах сменного состава или организованный диалог или метод диалогических сочетаний[1].

Однако отсутствие научного их обоснования, переоценка роли самостоятельности учащихся, недостаточное теоретическое осмысление сущности активного обучения, а так же ограниченность соответствующего методического обеспечения привели к отказу от их применения в учебном процессе. Дальнейшее развитие активные методы приобретают в конце 50-х — начала 60-х годов ХХ в., что было связано с работами советского дидакта Евгения Яковлевича Голанта, который предложил (в зависимости от способа деятельности учащихся в учебной деятельности) разделять методы обучения на «пассивные» и «активные». В 70-х годах ХХ в. активные методы вошли в имеющейся, в то время, классификации методов обучения и начали широко внедряться в систему образования. Их разработка связана с трудами Василия Сухомлинского, а в дальнейшем педагогической деятельностью Шалвы Амонашвили, Виктора Шаталова, Евгения Ильина. Это стало основой для возникновения теории и практики развивающего обучения.

Формы организации обучения и их развитие в дидактике

... в зависимости от задач и методов учебной работы, организуемой учителем. Об этом убедительно свидетельствует история развития организационных форм обучения. 1. Формы организации обучения и их развитие в дидактике Истории мировой педагогической мысли и практике обучения известны самые разнообразные формы организации обучения. Их возникновение, развитие, совершенствование и ...

Интерактивное обучение – это совокупность педагогических технологий, основанных на совместной деятельности, которые осуществляются средствами коммуникации и имеют проблемно-поисковую природу.

Современный период развития общества требует качественно нового уровня образования, который соответствовал бы международным стандартам. Сегодня в образовании ощутимый приоритет общечеловеческих ценностей. В соответствии с личностно-деятельностным подходом к организации учебного процесса в центре его находится тот, кто учится. Формирование личности и ее становление происходит в процессе обучения, когда соблюдаются определенные условия:

• создание позитивного настроя для обучения;
• ощущение равного среди равных;
• обеспечение позитивной атмосферы в коллективе для достижения общих целей;
• осознание личностью ценности коллективно сделанных умозаключений;

субъект обучения чувствует себя активным участником событий

В современном обществе источником знаний может выступать не только учитель, но и компьютер, телевизор, видео. Учащиеся должны уметь осмысливать полученную информацию, трактовать ее и применять в конкретных условиях; в то же время думать, понимать суть вещей, уметь выразить мысль. Именно этому способствуют интерактивные технологии.

«Интерактивный» (от англ. «inter» — взаимный и «act» — действовать) — способный к взаимодействию, диалогу. Интерактивное обучение — специфическая форма организации познавательной деятельности, которая имеет предполагаемую цель — создать комфортные условия обучения, при которых каждый ученик чувствует свою успешность, интеллектуальную состоятельность[2].

Главная черта интерактивного обучения — использование собственного опыта ученикам во время решения проблемных вопросов. Им предоставляется максимальная свобода мыслительной деятельности при построении логических цепей.

Использование современных инновационных технологий, в частности технологии интерактивного обучения, в значительной степени повышает эффективность учебного процесса, способствует высокому интеллектуальному развитию учащихся, обеспечивает овладение навыками саморазвития личности, возможностью думать, творить.

Преимущество интерактивного обучения в том, что учащиеся усваивают все уровни познания (знание, понимание, применение, оценка), в классах увеличивается количество учащихся, которые сознательно усваивают учебный материал. Ученики занимают активную позицию в усвоении знаний, растет их интерес в получении знаний.

1.2 Характеристика интерактивных методов обучения

Цель осуществления интерактивного обучения — диалог не ради взаимодействия детей, а взаимодействие ради проявления и реализации их индивидуальных особенностей.

Интерактивное обучение имеет свои преимущества и недостатки[3]:

• Преимущества: расширяют познавательные возможности ученика;
• как правило, высокий уровень усвоения знаний;
• учитель без труда может проконтролировать уровень усвоения знаний учениками;
• учитель имеет возможность раскрыться как организатор, консультант;
• партнерство между учителем и учениками и в ученическом коллективе.

Недостатки: на изучение определенной информации требуется значительное время; необходим другой подход в оценке; у учителя зачастую отсутствует опыт такого способа организации обучения; недостаток методических разработок уроков с использованием интерактивных методов.

«Методика воспитания и обучения» «Роль игры в обучении младших ...

... игр; Рассмотреть особенности данной методики обучения; Выявить актуальность и эффективность применения игры на занятиях в школьном образовательном учреждении; Определить связи использования игры с организацией проблемно-ориентированной развивающей среды для обучения школьников; Анализ и ...

Методы интерактивного обучения можно разделить на две большие группы: групповые и фронтальные. Первые предусматривают взаимодействие участников малых групп (2-6 человек), вторые — совместную работу и взаимообучение всего коллектива[4].

Групповые методы:

1.Работа в парах. Ученики работают в парах, выполняя задание.

2.Работа в тройках. По сути, это усложненная работа в парах. Лучше в тройках проводить обсуждение, обмен мнениями, подведение итогов или, наоборот, выделение непохожих мнений.

3.Изменяемые тройки. Этот метод немного сложнее: все тройки получают одно и то же задание, а после обсуждения один член тройки идет в следующую, еще один в предыдущую и знакомит членов вновь созданных троек с плюсом своей.

4.2+2=4. Две пары по отдельности работают над упражнением в течение определенного времени (2-3 минуты), доходят до общего решения, потом объединяются и делятся приобретенным.

5.Карусель. Учащиеся садятся в два круга — внутренний и внешний.

Внутренний круг неподвижен, внешний движется. Возможны два варианта использования метода — для дискуссии или для обмена информацией.

6.Работа в малых группах. Существенным является распределение ролей: «спикер» — руководитель группы (следит за регламентом во время обсуждения, зачитывает задачу, определяет докладчика, поощряет группу к работе), «секретарь» (ведет записи результатов работы, помогает при подведении итогов и их вынесении), «посредник» (следит за временем, поощряет группу к работе), «докладчик» (четко выражает мнение группы, докладывает о результатах работы группы).

Возможным является выделение экспертной группы из более сильных учеников. Они работают самостоятельно, а при объявлении результатов рецензируют и дополняют информацию[5].

Фронтальные методы[6]:

1.Большой круг. Ученики сидят в кругу и по очереди по желанию высказываются по определенным вопросам. Обсуждение продолжается, пока есть желающие высказаться. Учитель может взять слово после обсуждения.

2.Микрофон. Это разновидность большого круга. Ученики быстро по очереди высказываются по этой проблеме, передавая друг другу воображаемый «микрофон».

3.Незаконченные предложения. Несколько усложненный вариант большого круга: ответ ученика — это продолжение незаконченного предложения («можно сделать такой вывод», «я понял, что»).

4.Мозговой штурм. Общеизвестная технология, суть которой заключается в том, что все ученики по очереди высказывают абсолютно все мнения по этой проблеме. Высказанное не критикуется и не обсуждается до окончания высказываний[7].

5.Мозаика. Это метод, сочетающий и групповую, и фронтальную работу.

1.3 Интерактивные игры

Игры в интерактивном формате – это деятельность школьников или дошкольников, которая проходит под контролем учителя или воспитателя и направлена на решение поставленных задач с помощью коллективной работы. Такой формат игры позволяет обучить детей бесконфликтному и продуктивному общению со сверстниками, стать доброжелательными и терпимыми.

Среди всего многообразия игр с интерактивным элементом можно выделить следующие типы:

Игры по мотивам сказок пользуются популярностью в детских дошкольных учреждениях. Такие постановки понятны малышам, ведь в них фигурируют персонажи, известные им с детства. На всякий случай перед проведением подобной игры нужно провести подготовительное занятие, которое напомнит детям о героях истории. Наводящие вопросы от учителя помогут малышам вспомнить сюжет и смысл сказки.

Игры, знакомящие детей с окружающим миром. Для дошкольников берутся темы попроще: «Домашние животные», «Твердое-мягкое», «Кто живет в лесу» и т. д. Для школьников темы могут быть сложнее: игры на развитие самоконтроля, которые учат групповой поддержке и помогают лучше узнать одноклассников, выходят на первое место. С помощью стихотворной формы (она лучше всего воспринимается на слух) воспитатель здоровается с детьми и объясняет, в чем будут заключаться правила.

Игры с использованием презентаций или интерактивной доски удачно дополняют занятие и делают его более увлекательным и наглядным. Для школьников в презентацию могут быть включены коллективные задания на грамотность или арифметику, а для детей помладше – изображения животных и различные викторины. Однако, используя компьютер, не стоит забывать о главной цели интерактивной игры – налаживанию коммуникации между детьми.

Одной из ключевых задач исследования являлась разработка интерактивной игры для учеников начальной школы. Разработанная игра полностью соответствует требованиям интерактивного обучения и направлена не только на проверку знаний по математике, но и на социализацию обучающихся: игра способствует развитию коммуникативных навыков и умений. 

ЗАКЛЮЧЕНИЕ

Рассмотренные методы интерактивного обучения могут быть в значительной степени расширены. Во-первых, применение в различных формах обучения предоставляет им дополнительные оттенки. Во-вторых, одни из них могут выступать частью других. В-третьих, многие из перечисленных методов и методик представляют собой сложный комплекс действий, и их можно использовать не только целостно, но и частично.

Использование интерактивных методов обучения изменяет требования к работе педагога как на этапе подготовки к занятию, когда нужно подготовить большое количество материала (текстов, карт), так и во время самого занятия.

Одной из ключевых задач исследования являлась разработка интерактивной игры для учеников начальной школы. Разработанная игра полностью соответствует требованиям интерактивного обучения и направлена не только на проверку знаний по математике, но и на социализацию обучающихся: игра способствует развитию коммуникативных навыков и умений.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

[Электронный ресурс]//URL: https://psychoexpert.ru/referat/interaktivnyie-pedagogicheskie-tehnologii/

1. Блинов, А.О. Интерактивные методы в образовательном процессе [Текст]/ А.О. Блинов. – М.: Издательство «Научная библиотека», 2014. – 262 с.

2. Фридман, Л.М. Психологическая наука учителю [Текст] /Л.М. Фридман. – М.: Издательство «Просвещение», 1985. – 224с.

3. Лизинский, В.М. Приемы и формы в учебной деятельности [Текст]/ В.М. Лизинский. – М.: Издательский центр «Педагогический поиск», 2013. – 160с.

4. Смирнов, С.А.Педагогические теории, системы, технологии [Текст]/ С.А. Смирнов. – М.: Издательство «Просвещение», 2013. – 512 с.

5. Кукушин, В.С. Теория и методика обучения[Текст]: учебное пособие / В.С. Кукушин. – Ростов-на-Дону: Издательство «Феникс», 2005. – 474 с.

6. Коджаспирова, Г.М., Петров, К.В. Технические средства обучения и методика их использования [Текст] / Г.М. Коджаспирова, К.В. Петров. – М.: Издательский центр «Академия», 2014. – 256 с.

7. Коджаспирова, Г.М. Практикум и методические материалы [Текст] / Г.М. Коджаспирова. – М.: Издательство «Владос», 2003. – 416 с

ПРИЛОЖЕНИЕ

Методический паспорт интерактивной игры

Признаки интерактивности игры	Данную игру можно назвать интерактивной, так как она включает в себя такие признаки как: Работу в командах Использование интерактивной доски Всем участникам игры присуждаются определенные роли и ситуации Диалогичность общения Свобода выбора Создание ситуации успеха.
Класс	4 класс.
Место игры в образовательном процессе	Данная игра проводится в конце 2 четверти 4 класса.
Цель	Целью игры является повторение и закрепление изученного материала по математике за 4 года.
Задачи	Повысить коммуникативные навыки обучающихся. Научить достигать поставленные цели и задачи с помощью коллективной деятельности. Освоить основные жизненные правила общества. Повторить и закрепить изученный учебный материал. Развивать логическое мышление Развивать навыки взаимоконтроля и самоконтроля
Описание игры	В игре предусмотрено игровое табло, на котором размещены категории заданий, а так же количество баллов от 10 до 50, которые указывают на уровень сложности задания. К заданиям на 10 баллов относятся задания из курса математики для 1 класса: Выражение на сложение чисел в пределах первого десятка Выражение на вычитание чисел в пределах первого десятка Выражение на произведение чисел в пределах первого десятка Задание на знание названий геометрических фигур Задание на логику К заданиям на 20 баллов относятся задания из курса математики для 2 класса: Выражение на вычитание чисел в пределах третьего десятка Выражения на нахождение разности и частного чисел в пределах первого десятка Задание на знание названий геометрических фигур Задание на знание единиц измерения Задание на логику К заданиям на 30 баллов относятся задания из курса математики для 3 класса: Задание на составление и решение выражений на сложение и вычитание чисел в пределах второго десятка Задание на составление выражений из предложенных чисел в пределах первого десятка Задание на нахождение периметра четырехугольника Задание на знание единиц измерения Задание на логику К заданием на 40 баллов относятся задания из курса математики для 4 класса: Задание на составление и решение выражений на умножение и вычитание чисел в пределах второго десятка Задание на нахождение значения выражения Задание на нахождение длины сторон треугольника Задание на установление истинности утверждений Задание на логику К заданиям на 50 баллов относятся задания из курса математики для 4 класса олимпиадного уровня: Задание на составление и решение выражений на вычитание, деление и сложение Задание на установление закономерности последовательности чисел Задание на нахождение периметра треугольника Задание на нахождение величины «Время суток» Задание на логику
Ход игры	В начале игры учитель предлагает обучающимся поделиться на 2-3 команды. Затем каждая команда придумывает название, девиз, а так же выбирает капитана команды, который будет давать окончательный ответ. После того, как каждая команда представит себя, учитель записывает на доске названия команд и составляет таблицу, куда будут записываться баллы, которые обучающиеся будут получать за правильные ответы. Затем проводится жеребьевка, с помощью которой установится очередность отвечающих команд. Капитан команды, посовещавшись с командой, выбирает категорию и количество очков, на экране появляется задание и у всех команд есть 5 минут, по истечению которых, капитан команды должен дать окончательный ответ. Если ответ верный – команде присуждается выбранное количество очков, если ответ не верный – право ответа переходит к команде, капитан которой первый поднимет руку. В конце игры учитель подсчитывает количество очков у каждой команды и объявляет победителя.
	Слайд 1. Содержит в себе название содержимого материала, информацию о составителе, а так же необходимую кнопку для начала игры.
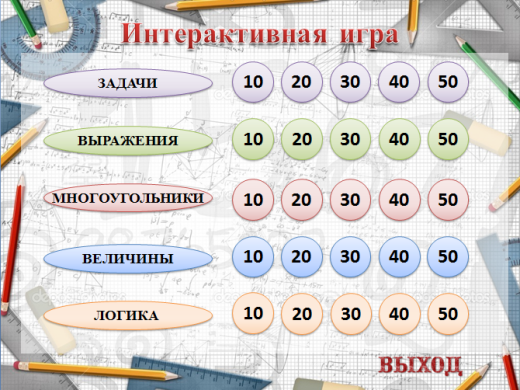
	Слайд 2. Содержит в себе игровое табло, где изображены названия категорий заданий: «задачи», «выражения», «многоугольники», «величины», «логика», а так же количество очков – от 10 до 50. В правом нижнем углу находится кнопка, которая позволяет перейти на первый слайд и закончить игру.
	Слайд 3. Содержит в себе информацию о категории задания и очках, получаемых за его выполнение. Задание: «На кустах распустилось 8 роз трёх цветов. Мама срезала красную, жёлтую и белую. Сколько роз осталось на кустах?». Нажав на значок в левом нижнем углу, выплывает правильное решение данного задания: «8-1-1-1=5 (роз)». Оранжевая стрелка в правом нижнем углу позволяет вернуться на игровое табло.
	Слайд 4. «Задачи» 20 У Маши было 36 рублей. После покупки мороженого у неё осталось 4 рубля. Сколько стоит мороженое? 36-4=32 (рубля)
	Слайд 5. «Задачи» 30 На одной полке 17 книг , а на другой – на 7 книг меньше. Сколько книг на двух полках? 17 – 7 = 10 ( книг ) – на второй полке 17+10=27 ( книг) – на двух полках
	Слайд 6. «Задачи» 40 В книге два рассказа. Один занимает 8 страниц, а другой в 3 раза больше. На сколько больше страниц занимает один рассказ, чем другой? 8 х 3 = 24 (страницы) — другой рассказ 24 – 8 = 16 (страниц) — разница в количестве страниц рассказов.
	Слайд 7. «Задачи» 50 В палатке продали за день 52 кг мандаринов, яблок на 12 килограммов меньше, а лимонов в 5 раз меньше, чем яблок. Сколько фруктов продали в палатке за день? 52 – 12 = 40 (кг) — продали яблок. 40:5= 8 (кг) — продали лимонов. 52+8+40 = 100 (кг) — продали фруктов.
	Слайд 8. «Выражения» 10 Найти сумму и произведение чисел 10 и 2 10+2=12 – сумма 10*2=20 — произведение
	Слайд 9. «Выражения» 20 Найти разность и частное чисел 12 и 12 12-12 = 0 – разность 12:12 = 1 — частное
	Слайд 10. «Выражения» 30 Используя числа 9, 36, 4, составьте четыре выражения. 4х9=36; 9х4=36; 36:4=9; 36:9=4
	Слайд 11. «Выражения» 40 Найдите значение выражения: (6х5+12:2):4= 1) 6х5=30; 2) 12:2=6; 3) 30+6=36; 4) 36:4=9
	Слайд 12. «Выражения» 50 Установите закономерность, продолжи ряд чисел: 7, 3, 10, 13, 23, …, …, … 13+23=46 23+46=69 46+69=115
	Слайд 13. «Многоугольники» 10 Как называется геометрическая фигура, если у неё три угла, три стороны и три вершины? Треугольник
	Слайд 14. «Многоугольники» 20 Как называется четырёхугольник, у которого все углы прямые? Прямоугольник
	Слайд 15. «Многоугольники» 30 Чему равен периметр четырёхугольника, если длина каждой стороны равна 3 дм? 3*4=12 (дм) — периметр четырёхугольника
	Слайд 16. «Многоугольники» 40 Периметр треугольника равен 27 дм. Какова длина каждой его стороны, если все они равны? 27:3=9 (дм) — длина каждой стороны треугольника
	Слайд 17. «Многоугольники» 50 В треугольнике АВС стороны АВ и ВС имеют одну и ту же длину, равную 8 дм, а сторона АС на 2 дм короче каждой из них. Вычислите периметр треугольника АВС. 8–2=6 (дм) – длина стороны АС. Р= 6+6+8=20 (дм)
	Слайд 18. «Величины» 10 Вставь пропущенные единицы длины: 60 см; 23 см; 2 дм; 2 метров
	Слайд 19. «Величины» 20 Что можно измерить в миллиметрах? *длину парты *толщину книги *длину божьей коровки * толщину тетради Длину парты лучше измерять в дм или см Длину божьей коровки, толщину тетради – в мм; Толщину книги в мм или см
	Слайд 20. «Величины» 30 Вставь пропущенные единицы измерения: в аквариуме помещается 15 …воды брат выше сестры на 12 … ребёнок весит 27… мороженое весит 100… 15 литров; 12 сантиметров; 27 килограммов; 100 граммов.
	Слайд 21. «Величины» 40 Найдите верные утверждения: 2дм3см=23дм 8дм4см=84см 8м=800см 9м=91дм 2дм 3 см = 23 дм –неверно, т.к 2дм3см= 23 см 8м4см=84см 8м= 800см 9м=91дм — неверно, 9м= 90дм
	Слайд 22. «Величины» 50 Золушка перебирает крупу. Который сейчас час, если с начала суток прошло в три раза больше времени, чем осталось? В сутках – 24 часа, так как осталось в три раза больше, чем осталось, значит всего – 4 части, если 24:4 = 6 (часов осталось) , прошло — 6х3= 18 часов.
	Слайд 23. «Логика» 10 Термометр за окном показывает 10 градусов мороза. А сколько градусов покажут 2 таких термометра? От количества градусников температура на улице не изменится и все они будут показывать 10 градусов.
	Слайд 24. «Логика» 20 В вазе лежали 5 леденцов и 8 ирисок. После того как Оля взяла тех и других конфет поровну, в вазе остались конфеты только одного сорта. Какого сорта эти конфеты и сколько их осталось? Оля взяла все леденцы и 5 ирисок, значит осталось 3 ириски.
	Слайд 25. «Логика» 30 К праздничному концерту второклассники подготовили 6 номеров – песни и танцы. Причём танцев было больше, чем песен. Сколько песен споют второклассники? Число 6 может состоять из двух неравных частей (1 и 5, 2 и 4) , песен может быть – 1 или 2.
	Слайд 26. «Логика» 40 Если к тем яблокам, которые лежат на тарелке, положить еще 6, то яблок станет в 2 раза больше, чем было. Сколько яблок было на тарелке сначала? Если станет в 2 раза больше , то станет -12 яблок, значит было сначала: 12 – 6 = 6 яблок.
	Слайд 27. «Логика» 50 Тридцатиметровую гирлянду мишуры разрезали на равные части, сделав при этом 5 разрезов. Какой длины получилась каждая часть. Если сделать 5 разрезов, получится 6 частей гирлянды, значит каждая часть равна 5 метрам (30 :6=5)